

 We did, yes.
We did, yes. Where are your friends? I want to congratulate them too!
Where are your friends? I want to congratulate them too! Ah, yes, funny story about that...
Ah, yes, funny story about that... All of the adults in our guild drank a lot of beer last night. Ray didn't, 'cause she's not an adult, but she sang a lot and made herself tired.
All of the adults in our guild drank a lot of beer last night. Ray didn't, 'cause she's not an adult, but she sang a lot and made herself tired. Oh dear. Kirtida always does say that explorers tend to enjoy a stiff drink...or three.
Oh dear. Kirtida always does say that explorers tend to enjoy a stiff drink...or three. Lady Harper is only able to assist me with business in town because she finds the taste of alcohol repugnant.
Lady Harper is only able to assist me with business in town because she finds the taste of alcohol repugnant. I like having my brain, too.
I like having my brain, too. It seems like you didn't have time to go gather food on your ship, then?
It seems like you didn't have time to go gather food on your ship, then? No. I made food last night, but Merula, Marlin, and I had to buy the ingredients.
No. I made food last night, but Merula, Marlin, and I had to buy the ingredients. Oh! Do you enjoy cooking, Miss Harper?
Oh! Do you enjoy cooking, Miss Harper? Mhm. A lot.
Mhm. A lot. How wonderful! Oh, we'll have to cook for each other sometime.
How wonderful! Oh, we'll have to cook for each other sometime. ...Maybe.
...Maybe.
 ...If finishing that simple mission is worthy of all this praise, I shudder to think how incompetent the average explorer must—
...If finishing that simple mission is worthy of all this praise, I shudder to think how incompetent the average explorer must— Can't hear ya, Bandage-Face!
Can't hear ya, Bandage-Face! I do have a name, Lady Wynne.
I do have a name, Lady Wynne. Ah, right, where's my mannahs?
Ah, right, where's my mannahs? No need to trouble yourself too much, just... I do wish people would ask for my name when they need to refer to me in the third-person. My name is Eine, by the way.
No need to trouble yourself too much, just... I do wish people would ask for my name when they need to refer to me in the third-person. My name is Eine, by the way. Einz, got it.
Einz, got it. ...Acceptable.
...Acceptable. Anyway, uh, I had somethin' to tell yas... Oh, doy. We got words from the Count—we can finally sell yas dem Ariadne threads. Every explorer gots ta have an—
Anyway, uh, I had somethin' to tell yas... Oh, doy. We got words from the Count—we can finally sell yas dem Ariadne threads. Every explorer gots ta have an— I'll take two.
I'll take two. But I didn't even tell yas what they do!
But I didn't even tell yas what they do! My moms were explorers.
My moms were explorers. Say no mores, I getcha. They taught ya well.
Say no mores, I getcha. They taught ya well.
 The box only says 1, but I bought two. I've gotten in the habit of always having two Ariadne threads in my pack at all times.
The box only says 1, but I bought two. I've gotten in the habit of always having two Ariadne threads in my pack at all times.Oh, right, I should explain what these are, for the newcomers. Ariadne threads are only usable while exploring and out of battle. They instantly warp you back to town. If you're playing on Casual, then you only need to keep one thread in your pack, because they're infinite use on that difficulty.
 A beautiful, blessed Ariadne Thread! In the flesh!
A beautiful, blessed Ariadne Thread! In the flesh! Hey, while ya here, this the first time either'a ya been up in a skyship?
Hey, while ya here, this the first time either'a ya been up in a skyship? No, I took a voyage on a commercial skyship here.
No, I took a voyage on a commercial skyship here. My first time.
My first time. Didja flip when ya tried flyin' on one?
Didja flip when ya tried flyin' on one? No.
No. Awwwwww. I like seein' explorers from outside flip out about skyships. The faces dey make, lemme tell ya.
Awwwwww. I like seein' explorers from outside flip out about skyships. The faces dey make, lemme tell ya.
 Here's a bunch of monster parts. And some rocks.
Here's a bunch of monster parts. And some rocks. Woah-ho-ho, dat ain't a bad haul for ya first expe-watchamacalits. I can give yas...71 en for it.
Woah-ho-ho, dat ain't a bad haul for ya first expe-watchamacalits. I can give yas...71 en for it. I take it none of these materials are particularly valuable.
I take it none of these materials are particularly valuable. Nah, not when every Tom, Dick, and Bruno's gots ta go through the Old Forest Mine ta get started.
Nah, not when every Tom, Dick, and Bruno's gots ta go through the Old Forest Mine ta get started.
 Anyways, here's what I can make for yas now.
Anyways, here's what I can make for yas now.Berund Atelier has the following new items in stock:
 Panzerstecher (24 ATK, +1 AGI): Made from
Panzerstecher (24 ATK, +1 AGI): Made from 2 Grasseater Legs (Grasseater Drop 1). Costs 160 en. Nirrti (29 ATK, 1 Slot): Made from
Nirrti (29 ATK, 1 Slot): Made from 2 Slates (Mine: Old Forest Mine). Costs 210 en. Leather Vest (22 DEF): Made from
Leather Vest (22 DEF): Made from 1 Roller Shell (Roller Drop 2). Costs 220 en.
 If these materials are so common, might I inquire why we're only able to purchase these now?
If these materials are so common, might I inquire why we're only able to purchase these now? Ev'ry guild's got their own stock'a mats. Wouldn't really be fair if one'a the bigger ones could, like, use all their cash ta buy all'a our weapons an' armor an' leave you guys high-an'-dry.
Ev'ry guild's got their own stock'a mats. Wouldn't really be fair if one'a the bigger ones could, like, use all their cash ta buy all'a our weapons an' armor an' leave you guys high-an'-dry. I...would hope that competition amongst guilds would extend no further than a friendly rivalry, but that is a wise policy nonetheless.
I...would hope that competition amongst guilds would extend no further than a friendly rivalry, but that is a wise policy nonetheless.

 I suspect that Lady Shelly might be interested in these rapiers... One panzerstecher, please.
I suspect that Lady Shelly might be interested in these rapiers... One panzerstecher, please. Comin' right up.
Comin' right up.
 Notice how the shop's stock of grasseater legs went down after we bought the panzerstetcher. Here's...one of the parts of EO4 that I don't like: all items in the shop, aside from starter equipment, consume materials on purchase. This is a bizarre step backwards from EO3, which required restocking for all non-starter consumables and any equipment made from FOE or boss drops, but at least let you buy equipment made from standard enemy drops without depleting Napier's stock.
Notice how the shop's stock of grasseater legs went down after we bought the panzerstetcher. Here's...one of the parts of EO4 that I don't like: all items in the shop, aside from starter equipment, consume materials on purchase. This is a bizarre step backwards from EO3, which required restocking for all non-starter consumables and any equipment made from FOE or boss drops, but at least let you buy equipment made from standard enemy drops without depleting Napier's stock.I suspect this change in EO4 was meant to balance the buffs given to the forging system, but that doesn't mean I have to like it. It also doesn't fix the actual problem with the EO3 shop, which was this awful system being applied to consumables, items you will be buying a lot of, and for whom limited stock just creates nothing but tedium for the player.
Astoundingly, EO4 somehow thought that the consumable grind in EO3 wasn't bad enough, and so not only did it nerf several key consumables, it also made stocking them even worse. Amrita IIIs? Not only did they nerf the actual TP restoration, in order to buy one, you need three of a monster drop. "That's not too bad," you might say, well too bad fucker that drop is a 20% chance. On an enemy that shows up in the middle of the postgame. "Well, I'll just use Amrita IIs, then," you might also say, to which I say "well too bad fucker" again, because Amrita IIs only restore 60 TP, an absolutely paltry amount even by the time you can first stock them.
I don't mean to get too ahead of myself here, but...man, I dislike EO4's decisions about how items and the shop work a lot. I don't think it's game-ruining, it's just bad design decisions. Thankfully, both of the Untolds learned from EO4's mistakes.
And then EO5 and EON both went back to literally the exact same system as EO4, probably because of the re-introduction of the concept of modifying weapons. Sigh...


 Criticizing a game I like is never fun. Let's move on.
Criticizing a game I like is never fun. Let's move on.As is the case with every EO game before EO5, spellcasters have different equipment priorities than other classes. And by that, I mean ATK does not influence TEC-based attacks or disable infliction at all, so classes that don't deal physical damage don't care about ATK at all. What they do care about stats and other types of bonuses on specific bits of equipment. In Xiaohu's case, that +1 TEC on this wand will give her a damage boost compared to if she kept using her dagger. It's a very small damage boost, but it is a damage boost.
One of the fun parts about EO4, actually, is that runemasters and arcanists actually don't particularly care for staves as weapons, past maybe the very earliest parts of the game. Daggers are where it's at! Sure, they've got lower ATK, but it's not like these magic-users care about that. What they do care about are bonuses, and daggers are often very modifiable—part of the trade-off with their lower ATK, in addition to their high equipment speed modifier, is that daggers come with more open forge slots than their contemporaries of other weapon types. Expect Xiaohu and Ray to both be rocking customized daggers before the 1st Land is over.

 Have a butcher's, mate. See, if it's good for slashin', that's a shiv, eh? But if it's a stabber, ye've got a shank.
Have a butcher's, mate. See, if it's good for slashin', that's a shiv, eh? But if it's a stabber, ye've got a shank. I'm going to avoid being a pedant here and say put that down, you are too young to have that in your hands!
I'm going to avoid being a pedant here and say put that down, you are too young to have that in your hands!

 Ace isn't really actually doing much after applying Taunt to themself right now, so... Sure, what the hell, let's get them a bit more damage. I've bought everything else I need.
Ace isn't really actually doing much after applying Taunt to themself right now, so... Sure, what the hell, let's get them a bit more damage. I've bought everything else I need.
 We're going to the bar.
We're going to the bar. Hm? Oh, right, Lady Kirtida did say—
Hm? Oh, right, Lady Kirtida did say—

 Yay. Hi, Kirtida.
Yay. Hi, Kirtida. Lady Harper...for the sake of my legs and lungs...hah, please, at least let me know when you're about to run off...
Lady Harper...for the sake of my legs and lungs...hah, please, at least let me know when you're about to run off... Okay. Sorry.
Okay. Sorry. It's no...trouble... I just...hah, need a moment to catch my breath...
It's no...trouble... I just...hah, need a moment to catch my breath... May I continue, or would you prefer I wait for you to recover?
May I continue, or would you prefer I wait for you to recover? By all means...go ahead...
By all means...go ahead... You have already been able to get advice from our patrons, I know, but you may also accept quests from us now. Completion of these quests is met with commensurate rewards. Many explorers enjoy passing time in this way. A request I think to be perfect for you was only just posted. Might I ask that you look it over?
You have already been able to get advice from our patrons, I know, but you may also accept quests from us now. Completion of these quests is met with commensurate rewards. Many explorers enjoy passing time in this way. A request I think to be perfect for you was only just posted. Might I ask that you look it over? Hmm...
Hmm... Do note that requests will mount up over time. Be sure to check the notice board every so often.
Do note that requests will mount up over time. Be sure to check the notice board every so often. We will...remember to do so...
We will...remember to do so... ...Dear me. Shall I get you some water, sir?
...Dear me. Shall I get you some water, sir? That would be...much appreciated...
That would be...much appreciated...
 Are you okay, Eine?
Are you okay, Eine? Yes, the water helped immensely.
Yes, the water helped immensely. Good. I'm glad you're okay.
Good. I'm glad you're okay. Thank y—
Thank y— Aged baboon hunter:
Aged baboon hunter: A-ah, Lady Harper, I'm not...seeing things, correct?
A-ah, Lady Harper, I'm not...seeing things, correct? ...That man has a baboon's head for a hat. That's...scary.
...That man has a baboon's head for a hat. That's...scary. Eh?! What's that, kids?!
Eh?! What's that, kids?! Aaaaahhhh! Loud!
Aaaaahhhh! Loud! We can hear you fine, sir. My apologies, we did not mean to gawk at—
We can hear you fine, sir. My apologies, we did not mean to gawk at— What, my hat?! Yeah, it's real high fashion! Bwahahahaha!
What, my hat?! Yeah, it's real high fashion! Bwahahahaha! If you...say so.
If you...say so. You kids look like explorers! You fought that damn monkey?! The Angry Baboon on B1F of the Lush Woodlands?!
You kids look like explorers! You fought that damn monkey?! The Angry Baboon on B1F of the Lush Woodlands?! Nnnnnn...
Nnnnnn... W-We have yet to step foot in the Lush Woodlands, sir.
W-We have yet to step foot in the Lush Woodlands, sir. Well, be careful when you do! It's the number one killer of rookie explorers in this town! You can't just swing at it blindly! If you're gonna take that thing on, don't skimp on defense! You might even wanna think about running away! Because if you die, that's all she wrote! Bwahahahaha!
Well, be careful when you do! It's the number one killer of rookie explorers in this town! You can't just swing at it blindly! If you're gonna take that thing on, don't skimp on defense! You might even wanna think about running away! Because if you die, that's all she wrote! Bwahahahaha! Thank you, sir, we'll be going now.
Thank you, sir, we'll be going now. ...He's too loud...
...He's too loud... The baboon hunter isn't kidding, Angry Baboons are not to be trifled with.
The baboon hunter isn't kidding, Angry Baboons are not to be trifled with.Grizzled, one-eyed man:
 Ah, good day, s— My apologies, "crusty guy."
Ah, good day, s— My apologies, "crusty guy." Hey, you're learning. Gonna guess your guild finished the mission?
Hey, you're learning. Gonna guess your guild finished the mission? Indeed.
Indeed. 'Grats. You want some more advice before you go any deeper?
'Grats. You want some more advice before you go any deeper? We'd be happy to listen.
We'd be happy to listen. Smart. So... While you were on the mission, did you pay any attention to your monster sense?
Smart. So... While you were on the mission, did you pay any attention to your monster sense? Beg pardon?
Beg pardon? Oh, the danger color.
Oh, the danger color. The what?
The what? I saw different colors when monsters were near. Blue, green, red.
I saw different colors when monsters were near. Blue, green, red. ...You're one-of-a-kind, little miss. Us explorers, we've got a good sense for when monsters are nearby. Their breathing, them snapping twigs when they walk, even just their...presence, sort of, we pick up on that unconsciously. I've never heard of someone's monster sense doing that to them, though.
...You're one-of-a-kind, little miss. Us explorers, we've got a good sense for when monsters are nearby. Their breathing, them snapping twigs when they walk, even just their...presence, sort of, we pick up on that unconsciously. I've never heard of someone's monster sense doing that to them, though. This is meant to explain what that colored circle in the bottom right of the top screen is, if you hadn't already picked up on it. It shifts colors, starting at blue and ending at red, to show how close you are to entering a battle.
This is meant to explain what that colored circle in the bottom right of the top screen is, if you hadn't already picked up on it. It shifts colors, starting at blue and ending at red, to show how close you are to entering a battle. What else, what else... Oh, right. You saw the Nomad Baboon at the Old Forest Mine. You had to have.
What else, what else... Oh, right. You saw the Nomad Baboon at the Old Forest Mine. You had to have. The one with the moustache and styled hair?
The one with the moustache and styled hair? Exactly. Those kinds of enemies—
Exactly. Those kinds of enemies— FOEs.
FOEs. There's a name for them? Out here, we just call them "big pains in the ass." They're damned tough. It's usually best to just run away...but even that takes some know-how. Some monsters don't care about you, they're just following their path. And some will actively chase you. It sounds obvious, but different types of monsters have different patterns or senses, so you can't generalize. But if you learn to anticipate their moves, you should start to figure out how to get the advantage.
There's a name for them? Out here, we just call them "big pains in the ass." They're damned tough. It's usually best to just run away...but even that takes some know-how. Some monsters don't care about you, they're just following their path. And some will actively chase you. It sounds obvious, but different types of monsters have different patterns or senses, so you can't generalize. But if you learn to anticipate their moves, you should start to figure out how to get the advantage. A...second tutorial about FOEs, for some reason.
A...second tutorial about FOEs, for some reason.Lazy maintenance worker:
 You cleared the mission from the Outland Count?
You cleared the mission from the Outland Count? Yes.
Yes. Then you should get started taking requests. Request rewards are an important source of income for explorers. The system's win-win for everyone. You can even build experience doing them, if you need to train a bit. Check the quest board when you can.
Then you should get started taking requests. Request rewards are an important source of income for explorers. The system's win-win for everyone. You can even build experience doing them, if you need to train a bit. Check the quest board when you can. That does sound reasonable.
That does sound reasonable. Some of the real straight-edge types only come to this bar to get quests, then immediately leave. Squares, if you ask me.
Some of the real straight-edge types only come to this bar to get quests, then immediately leave. Squares, if you ask me. Then, are you here for...I believe the saying is "both business and pleasure?"
Then, are you here for...I believe the saying is "both business and pleasure?" Business? Pshaw. I just come here every so often to check out the barmaid. I mean, look at her.
Business? Pshaw. I just come here every so often to check out the barmaid. I mean, look at her. She certainly is serving drinks.
She certainly is serving drinks. No, kid, I mean... Y'know, look at her.
No, kid, I mean... Y'know, look at her. ...Hmph. If you're referring to her physical appearance, then I can't say that I particularly care.
...Hmph. If you're referring to her physical appearance, then I can't say that I particularly care. Cooking guild member:
Cooking guild member: Do you cook?
Do you cook? What gave it away? The hat?
What gave it away? The hat? Yes.
Yes. ...Right, dumb question. You got a skyship? If so, be very careful of the tornadoes you come across. Come into contact with one, and you'll lose all your food... The loss of food before anyone has had a chance to taste it is a tragedy no one should have to bear.
...Right, dumb question. You got a skyship? If so, be very careful of the tornadoes you come across. Come into contact with one, and you'll lose all your food... The loss of food before anyone has had a chance to taste it is a tragedy no one should have to bear. I'd be more afraid of injuries to myself and my guildmates...
I'd be more afraid of injuries to myself and my guildmates... Losing food is a big problem, too.
Losing food is a big problem, too. She gets me. Better to throw it to the kangaroos wandering the land! They enjoy vegetables, I happen to know. Ebony Carrots don't have any other use but to lure those kangaroos anyway. You can even scatter them as bait.
She gets me. Better to throw it to the kangaroos wandering the land! They enjoy vegetables, I happen to know. Ebony Carrots don't have any other use but to lure those kangaroos anyway. You can even scatter them as bait. Oh, that must be what the foodapult the Count bequeathed us is for!
Oh, that must be what the foodapult the Count bequeathed us is for! Yep. Those big monsters—
Yep. Those big monsters— FOEs.
FOEs. Oh, that's much easier to say. FOEs are just like any other animal: put food they like in front of them, and they'll just immediately start chomping. Flying a skyship's a lot easier when you don't have an angry kangaroo constantly on your tail.
Oh, that's much easier to say. FOEs are just like any other animal: put food they like in front of them, and they'll just immediately start chomping. Flying a skyship's a lot easier when you don't have an angry kangaroo constantly on your tail. Old soldier raising a mug:
Old soldier raising a mug: Hail, explorers. Take a seat and have a drink, why don't you?
Hail, explorers. Take a seat and have a drink, why don't you?
 Water, please.
Water, please. Heh. An explorer's curiosity certainly is insatiable... If they have an errand, they'll even head out at night. Since you seem to just be starting out, let me give you fair warning. Be careful when exploring at night. You're likely to run into terrifying beasts you don't see during the day. It takes some getting used to.
Heh. An explorer's curiosity certainly is insatiable... If they have an errand, they'll even head out at night. Since you seem to just be starting out, let me give you fair warning. Be careful when exploring at night. You're likely to run into terrifying beasts you don't see during the day. It takes some getting used to. This...isn't really a thing, after the 1st Land. EO2 and EO3 experimented a lot with having the time of day have large effects on random encounter groups, and even FOE behavior, but EO4 really tamped down on that. EOU, to my recollection, doesn't have the time of day really affect anything, EO2U has one specific FOE change their behavior at night, EO5's 3rd Stratum's gimmick changes based on day/night, but that's kind of it.
This...isn't really a thing, after the 1st Land. EO2 and EO3 experimented a lot with having the time of day have large effects on random encounter groups, and even FOE behavior, but EO4 really tamped down on that. EOU, to my recollection, doesn't have the time of day really affect anything, EO2U has one specific FOE change their behavior at night, EO5's 3rd Stratum's gimmick changes based on day/night, but that's kind of it.Canny medic Sophie:
 Hail, explorers.
Hail, explorers. Hail, medic lady.
Hail, medic lady. To survive in the labyrinth, you need to know your limitations. If you have any questions for me, don't hesitate to ask. I'm usually here, too.
To survive in the labyrinth, you need to know your limitations. If you have any questions for me, don't hesitate to ask. I'm usually here, too. Sophie has a lot of very basic tutorials, but she does actually have some very important advice pertaining to mechanics you might not otherwise be aware of. The first is equipment speed, which I already talked about. The other one...
Sophie has a lot of very basic tutorials, but she does actually have some very important advice pertaining to mechanics you might not otherwise be aware of. The first is equipment speed, which I already talked about. The other one... Hmm... What's, in your opinion, your most obscure advice? Something you think most others would gloss over.
Hmm... What's, in your opinion, your most obscure advice? Something you think most others would gloss over. Good ask. Okay, did you know enemies get used to bindings and ailments over time? It's hard to make the same one stick twice. That's why it's better to have a variety of bindings and ailments at your disposal.
Good ask. Okay, did you know enemies get used to bindings and ailments over time? It's hard to make the same one stick twice. That's why it's better to have a variety of bindings and ailments at your disposal. Hmm... Ailments of the body, I would've assumed that for. I had no idea that would apply to bindings, though.
Hmm... Ailments of the body, I would've assumed that for. I had no idea that would apply to bindings, though. That gets a lot of people, can be real hard to notice. Some of the real old-timers around here have told me about monsters that kinda don't... Hm, how do I put it...
That gets a lot of people, can be real hard to notice. Some of the real old-timers around here have told me about monsters that kinda don't... Hm, how do I put it... By the context, I would assume "build up a natural immunity?"
By the context, I would assume "build up a natural immunity?" Close, but it's more like...monsters that just don't get any more used to bindings. I've never seen one myself, but if binds seem really important—like, really really important—then I'd guess that'd have something to do with it.
Close, but it's more like...monsters that just don't get any more used to bindings. I've never seen one myself, but if binds seem really important—like, really really important—then I'd guess that'd have something to do with it. Wonderful advice, madam. Thank you.
Wonderful advice, madam. Thank you. What Sophie is talking about here is accumulative resistance, an inherent property of both player characters and enemies, introduced in EO3. Simply put, every time something becomes afflicted with an ailment, or has a body part bound, they lose 30% vulnerability to that specific disable. For example, if an enemy has a 50% vulnerability to poison—meaning that any chance of inflicting poison on them is multiplied by 0.5—then, after they have poison inflicted on them once, their vulnerability to poison becomes 20%. If they have poison inflicted on them again, their vulnerability to poison will become 0%, making them completely immune to being afflicted with poison.
What Sophie is talking about here is accumulative resistance, an inherent property of both player characters and enemies, introduced in EO3. Simply put, every time something becomes afflicted with an ailment, or has a body part bound, they lose 30% vulnerability to that specific disable. For example, if an enemy has a 50% vulnerability to poison—meaning that any chance of inflicting poison on them is multiplied by 0.5—then, after they have poison inflicted on them once, their vulnerability to poison becomes 20%. If they have poison inflicted on them again, their vulnerability to poison will become 0%, making them completely immune to being afflicted with poison.Now, it's worth noting that the accumulative resistance system in EO3—and, by extension, EO4—is somewhat primitive. Namely, accumulative resistance does not naturally wear off as a battle goes on. Starting from EOU on, accumulative resistance wears at a rate of 7% per turn with each turn, though the actual resistance it provides is higher, at 50%, to compensate for that. To wit, it takes eight turns for a stack of accumulative resistance to completely wear off, though by the seventh turn, it'll be down to a whopping 1% vulnerability reduction.
In EO3, there was absolutely no way to remove accumulative resistance. Zero, zip, nada. You inflicted a disable on an enemy, that's it, they're just more permanently resistant to it. In EO4, there is exactly one way to remove accumulative resistance from enemies: Releasal Spell, which arcanists can learn once they unlock their Master skills. Releasal Spell is pleasingly simple: it just resets all of an enemy's accumulative resistances to 0. That's it. Costs a lot of TP, but if your party relies a lot on disables, especially binds, and can't kill an enemy quickly, it's a godsend.
If you feel like this is the game being a bit unfair to the player, remember: player characters have accumulative resistance, too. Exact same mechanics as enemies. You get to benefit just as much as enemies do, with the caveat that death will immediately reset all of a character's accumulative resistance.
Also, all that stuff about special enemies isn't actually mentioned in the original text that I based this on, but it's important to note anyways. There's a handful of enemies—including two bosses—that do not gain accumulative resistance to binds. Don't worry, when they come up, there'll be a special note in the enemy overview letting you know that important fact. It's strange the game doesn't mention this, it has a pretty big impact on strategies for taking on both of the applicable bosses.

 Right, quests, the thing most people actually come to the bar for. They've already been explained, so let's just get going.
Right, quests, the thing most people actually come to the bar for. They've already been explained, so let's just get going.Supply request:
 We'll take the food one.
We'll take the food one. Ah, that one is good for new explorers. A group of soldiers are exploring the east side of the Windy Plains. But they lack the food to carry on. So your task would be to gather food and drop it off for them. Their camp is in the forest. I was given to understand that it is in an open area. Freshness is important in food, so you must find and deliver it in one trip.
Ah, that one is good for new explorers. A group of soldiers are exploring the east side of the Windy Plains. But they lack the food to carry on. So your task would be to gather food and drop it off for them. Their camp is in the forest. I was given to understand that it is in an open area. Freshness is important in food, so you must find and deliver it in one trip. Simple enough.
Simple enough. The Outland Count's task:
The Outland Count's task: Oh, the Count makes requests here?
Oh, the Count makes requests here? For matters that are not urgent enough to be missions, yes. For this one in particular... He wants you to search for a small
For matters that are not urgent enough to be missions, yes. For this one in particular... He wants you to search for a smallgrove of kapok trees. You can learn more by talking to him at the Grand Court.
 ...Another entry on mine and Harper's to-do list, then. I do hope the others appreciate us handling this.
...Another entry on mine and Harper's to-do list, then. I do hope the others appreciate us handling this. Mm.
Mm. L-Lady Harper, you're hugging me.
L-Lady Harper, you're hugging me. Mhm.
Mhm. Might I ask why...?
Might I ask why...? Because you're helping us a lot.
Because you're helping us a lot. ...Well. Thank you.
...Well. Thank you. Atelier request:
Atelier request: Forgive the interruption, but the Berund Atelier has posted a request as well, if your guild is interested.
Forgive the interruption, but the Berund Atelier has posted a request as well, if your guild is interested. We are.
We are. They are keenly interested in materials for a sword. They can supply you with more details of the task at the Atelier.
They are keenly interested in materials for a sword. They can supply you with more details of the task at the Atelier. We'll make sure to stop by there again.
We'll make sure to stop by there again. That is all of the requests I have available, then. I await your swift return.
That is all of the requests I have available, then. I await your swift return.

 Good morning, Sir Count. We've accepted the request you posted at the Dancing Peacock.
Good morning, Sir Count. We've accepted the request you posted at the Dancing Peacock. Ah, it was your guild that accepted? That's very reassuring, you all did quite well with your first mission. Are you familiar with kapoks?
Ah, it was your guild that accepted? That's very reassuring, you all did quite well with your first mission. Are you familiar with kapoks? No. We have a lot of palm trees and regular trees back home, though.
No. We have a lot of palm trees and regular trees back home, though. Kapok trees are not grown for food, but for their several other uses—one can make fiber from them, that sort of thing. There is a place in these Windy Plains where many kapoks grow; I want you to search for it. Rumor has it that it's somewhere on the northern side of the Windy Plains. The A-2 region sounds likely.
Kapok trees are not grown for food, but for their several other uses—one can make fiber from them, that sort of thing. There is a place in these Windy Plains where many kapoks grow; I want you to search for it. Rumor has it that it's somewhere on the northern side of the Windy Plains. The A-2 region sounds likely. Ah, far north and a bit west.
Ah, far north and a bit west. Now then, if you do happen to find the kapok grove, return here and tell me its coordinates.
Now then, if you do happen to find the kapok grove, return here and tell me its coordinates. We will be on the lookout, sir.
We will be on the lookout, sir. If you already know where the kapok grove is, or if you cheated and looked up where it is online, you can just immediately tell the Count. What fun is that, though?
If you already know where the kapok grove is, or if you cheated and looked up where it is online, you can just immediately tell the Count. What fun is that, though?
 We're back. Ah, good, some of you have woken up.
We're back. Ah, good, some of you have woken up. Nnngh, my head... Morning, you two.
Nnngh, my head... Morning, you two. Man, all those mugs, and we barely even scratched the surface of the fabled Stash of the Heedless Blaze.
Man, all those mugs, and we barely even scratched the surface of the fabled Stash of the Heedless Blaze. ...
... Lady Xiaohu? Are you—
Lady Xiaohu? Are you— Yes. I am fine. Please do not talk to me right now.
Yes. I am fine. Please do not talk to me right now. O-Oh. My apolo—
O-Oh. My apolo— Eine, please. I am not trying to be rude, but, while I enjoy a nice round of drinking, my veisalgia does not respond well to others talking to me.
Eine, please. I am not trying to be rude, but, while I enjoy a nice round of drinking, my veisalgia does not respond well to others talking to me. ...
... Eine nods.
Eine nods. Thank you.
Thank you. I do not wish to disturb anyone, but we have business to attend to today. Lady Shelly, is it particularly noticeable when this ship is in motion?
I do not wish to disturb anyone, but we have business to attend to today. Lady Shelly, is it particularly noticeable when this ship is in motion? You kidding me? You think my crew would've built the Air B'n'B, a god among skyships, without giving it—aaagh—some world-class stabilization?
You kidding me? You think my crew would've built the Air B'n'B, a god among skyships, without giving it—aaagh—some world-class stabilization? No, but it's good to have that confirmed. Now, ah... I don't feel particularly confident piloting this, but I assume no-one here is in the mood to pilot.
No, but it's good to have that confirmed. Now, ah... I don't feel particularly confident piloting this, but I assume no-one here is in the mood to pilot. Nah, don't worry, I've got it. Piloting with a hangover sucks, but I've done more than my fair share of it.
Nah, don't worry, I've got it. Piloting with a hangover sucks, but I've done more than my fair share of it. Without—
Without— Without crashing, yes. Chill a bit, Eine, I'd sooner get my sword arm chopped off than do anything that would put my comrades in any real danger.
Without crashing, yes. Chill a bit, Eine, I'd sooner get my sword arm chopped off than do anything that would put my comrades in any real danger. ...I will let that sentiment reassure me, then.
...I will let that sentiment reassure me, then.
 Let's mosey.
Let's mosey.



 Man, now this is a hell of a gorgeous day.
Man, now this is a hell of a gorgeous day. Oooooh.
Oooooh. Not a cloud to be found in the sky.
Not a cloud to be found in the sky. The skyship you have christened Air B'n'B rises from the city gates. As you would expect from the Windy Plains, strong gusts of wind blow across the skies. Some of the stronger winds seem likely to sway the Air B'n'B from her course...
The skyship you have christened Air B'n'B rises from the city gates. As you would expect from the Windy Plains, strong gusts of wind blow across the skies. Some of the stronger winds seem likely to sway the Air B'n'B from her course... Oh, yeah, I mentioned that my babe has a lot of stabilization, but that doesn't mean it won't get a little turbulent if we go through rough winds.
Oh, yeah, I mentioned that my babe has a lot of stabilization, but that doesn't mean it won't get a little turbulent if we go through rough winds. As much as I probably do not need to say this to an experienced pilot, please do not fly into any rough winds. For my sake, if nothing else.
As much as I probably do not need to say this to an experienced pilot, please do not fly into any rough winds. For my sake, if nothing else. Ah. Not so good with flying, huh?
Ah. Not so good with flying, huh? ...We are rather high up.
...We are rather high up. Would you believe me if I told you some of my best mates had acrophobia?
Would you believe me if I told you some of my best mates had acrophobia? I'd...believe it, but that would not make me any less surprised.
I'd...believe it, but that would not make me any less surprised. Well, they did, and I still trusted them with my life, even when we had to fight while airborne. So... I dunno, you're not alone. Take some comfort in that, I guess.
Well, they did, and I still trusted them with my life, even when we had to fight while airborne. So... I dunno, you're not alone. Take some comfort in that, I guess. ...Yggdrasil is really big.
...Yggdrasil is really big. It's not the "tree of life" for nothing. Anyway, what's up, what'd you get for us to do today?
It's not the "tree of life" for nothing. Anyway, what's up, what'd you get for us to do today? We have two requests that require sailing around the Windy Plains, but...perhaps we should spend some time mapping this area out.
We have two requests that require sailing around the Windy Plains, but...perhaps we should spend some time mapping this area out. —!
—! Well, Harper? You up for mapping something besides a labyrinth?
Well, Harper? You up for mapping something besides a labyrinth? Mhm, mhm, mhm!
Mhm, mhm, mhm! Nice. Well, just lemme know where to go to fill that thing in.
Nice. Well, just lemme know where to go to fill that thing in. Welcome to the overworld. Well, the first overworld of four. We'll be using this to travel to different caves—smaller labyrinths, like the Old Forest Mine—as well as to the main maze, the Lush Woodlands. While we're traveling on the overworld, we can also collect food from random points on the map, and also get into fights with FOEs. Overworld FOEs are a cut above any FOE you'll find in a labyrinth, so do take care around them.
Welcome to the overworld. Well, the first overworld of four. We'll be using this to travel to different caves—smaller labyrinths, like the Old Forest Mine—as well as to the main maze, the Lush Woodlands. While we're traveling on the overworld, we can also collect food from random points on the map, and also get into fights with FOEs. Overworld FOEs are a cut above any FOE you'll find in a labyrinth, so do take care around them.

 Overworld tiles are automatically filled in on the map as we move around, which is much appreciated. Additionally, overworld maps also very clearly mark which tiles we have vision over. We can't see what food or, importantly, FOEs, are on tiles that we haven't gained vision over yet. This same restriction applies to the main labyrinths, but the game doesn't actually visually indicate what tiles you have vision over, a flaw fixed with EOU. Note that once you've gotten vision over a tile, you have vision over it forever. Additionally, vision is not obstructed by physical obstacles besides, well, the end of the map data.
Overworld tiles are automatically filled in on the map as we move around, which is much appreciated. Additionally, overworld maps also very clearly mark which tiles we have vision over. We can't see what food or, importantly, FOEs, are on tiles that we haven't gained vision over yet. This same restriction applies to the main labyrinths, but the game doesn't actually visually indicate what tiles you have vision over, a flaw fixed with EOU. Note that once you've gotten vision over a tile, you have vision over it forever. Additionally, vision is not obstructed by physical obstacles besides, well, the end of the map data.

 There's some quite large fish directly below us.
There's some quite large fish directly below us. Mega-Net, go!
Mega-Net, go!
 Alright, we've got fish in the freezer now.
Alright, we've got fish in the freezer now. The... The freezer? I have to imagine those are exceptionally heavy.
The... The freezer? I have to imagine those are exceptionally heavy. Just means my crew had to figure out how to give the Air B'n'B more lift.
Just means my crew had to figure out how to give the Air B'n'B more lift. This ship is a marvel of modern engineering...
This ship is a marvel of modern engineering... Food is a pretty big part of overworld exploration. Every day, random food points will spawn on the overworld. You can fly over to them, press A, and there, you've got food. It's vaguely like fishing in EO3? Except it's far less frustrating, and can even provide you with benefits during labyrinth exploration.
Food is a pretty big part of overworld exploration. Every day, random food points will spawn on the overworld. You can fly over to them, press A, and there, you've got food. It's vaguely like fishing in EO3? Except it's far less frustrating, and can even provide you with benefits during labyrinth exploration.There's three things you can do with food: eat it, use it as bait for FOEs, or automatically sell it once you return to town. There is zero consequence to eating food—unless you eat poison food, I guess. The benefits range from stat boosts to damage/disable resistance increases to battle reward increases, you get the idea.
A given food spot has a maximum number of food items you can gather from it. For each possible food, the game then rolls to see if you got the standard food for that point, with the chance being either 90%, 95%, or 97%. If the standard roll fails, you have an 80% chance to get the rare food instead. If that fails, then you get nothing.
Food spots also have a small chance, usually ranging from 10% to 20%, of being a rare spot, which changes their standard food, and increases the chance of getting the rare food. Rare point standard food can have any of the following chances to be rolled for: 75%, 80%, 85%.
Riveting stuff, huh? I think it's neat, anyways. Let's look at the food you can find in the 1st Land! For each food point type, the items are organized: normal point standard, rare point standard, rare.
- Meat:
 Tharsis Buffalo: +1 STR. Sells for 7 en.
Tharsis Buffalo: +1 STR. Sells for 7 en. Red Horned Ox: +2 STR, +1 VIT. Sells for 15 en.
Red Horned Ox: +2 STR, +1 VIT. Sells for 15 en. Black Taurus: +3 STR, +1 VIT. Multiplies rare breed chance by 3x. Sells for 80 en.
Black Taurus: +3 STR, +1 VIT. Multiplies rare breed chance by 3x. Sells for 80 en.- Poultry:
 Tharsis Duck: +1 TEC. Sells for 8 en.
Tharsis Duck: +1 TEC. Sells for 8 en. Heavy Duck: +2 TEC, +1 AGI. Sells for 20 en.
Heavy Duck: +2 TEC, +1 AGI. Sells for 20 en.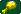 Golden Goose: +3 TEC, +1 AGI. Increases EXP gained in battle by 20%. Sells for 90 en.
Golden Goose: +3 TEC, +1 AGI. Increases EXP gained in battle by 20%. Sells for 90 en.- If fed to an FOE, the FOE will become a rare breed.
- Fish:
 Gray Trout: +1 AGI. Increases all party members' volt resistances by 10%. Sells for 10 en.
Gray Trout: +1 AGI. Increases all party members' volt resistances by 10%. Sells for 10 en. Red Kokanee: Increases all party members' ice and volt resistances by 15%. Sells for 25 en.
Red Kokanee: Increases all party members' ice and volt resistances by 15%. Sells for 25 en. Sakura Trout: +10 TP. Increases all party members' ice and volt resistances by 20%. Sells for 100 en.
Sakura Trout: +10 TP. Increases all party members' ice and volt resistances by 20%. Sells for 100 en.- Vegetable:
 Baby Carrot: +1 LUC. Increases all party members' blind resistance by 10%. Sells for 5 en.
Baby Carrot: +1 LUC. Increases all party members' blind resistance by 10%. Sells for 5 en. Sugar Carrot: +2 LUC. Increases all party members' blind resistance by 20%. Adds 8% to monster drop chances. Sells for 10 en.
Sugar Carrot: +2 LUC. Increases all party members' blind resistance by 20%. Adds 8% to monster drop chances. Sells for 10 en. Ebony Carrot: Poisoned. Sells for 70 en.
Ebony Carrot: Poisoned. Sells for 70 en.- If the party has a medic who knows Toxin Study, the food grants: +3 LUC. Increases all party members' blind and panic resistances by 30%.
- If a party without Toxin Study eats the food, all party members will take 40 damage.
- If an FOE eats the food, and the party engages it in combat, the FOE will be afflicted with poison at the start of battle. The poison deals 41 to 50 damage.
 The ice and volt resistances are pretty worthless. One enemy in any of the 1st Land labyrinths can deal volt damage, and one other enemy can deal ice damage. Otherwise, this stuff's fairly okay. Meat tends to be the most useful food type in my experience, since a significant amount of classes rely on STR for their damage.
The ice and volt resistances are pretty worthless. One enemy in any of the 1st Land labyrinths can deal volt damage, and one other enemy can deal ice damage. Otherwise, this stuff's fairly okay. Meat tends to be the most useful food type in my experience, since a significant amount of classes rely on STR for their damage.Oh, by the way, if you want to 100% the game, you'll need to get every food item at least once.


 Drawing maps without monsters being near is fun.
Drawing maps without monsters being near is fun. There's no random encounters out on the overworld, just FOEs. Long as you don't run into an FOE, feel free to wander around as much as you want.
There's no random encounters out on the overworld, just FOEs. Long as you don't run into an FOE, feel free to wander around as much as you want.

 Another skyship, starboard side.
Another skyship, starboard side. Well well well. Done your research on ships?
Well well well. Done your research on ships? Does reading adventure stories count as research?
Does reading adventure stories count as research? Sure. Anyway, they look friendly enough. Wanna go talk to them, Harper?
Sure. Anyway, they look friendly enough. Wanna go talk to them, Harper? Mhm.
Mhm.

 Its sails are a deep blue. The figure aboard the skyship notices your coming and emerges from the gondola. You mark them as a person clad in steel armor, who bows politely to you.
Its sails are a deep blue. The figure aboard the skyship notices your coming and emerges from the gondola. You mark them as a person clad in steel armor, who bows politely to you.
 Good day, Liege Kirjonen.
Good day, Liege Kirjonen. I am the most lowly of the Holy Rune Knights who serve King Bjornstad. I am pleased to make your acquaintance.
I am the most lowly of the Holy Rune Knights who serve King Bjornstad. I am pleased to make your acquaintance. Hi, Kirjonen.
Hi, Kirjonen. Happy to meet you, though I've gotta ask how you already know about us.
Happy to meet you, though I've gotta ask how you already know about us. I am familiar with most of the explorers of Tharsis. It takes up no small amount of time, but I find the benefits outweigh the costs. By the by, I have a request. Would you have any sakura trouts? If so, I propose a trade.
I am familiar with most of the explorers of Tharsis. It takes up no small amount of time, but I find the benefits outweigh the costs. By the by, I have a request. Would you have any sakura trouts? If so, I propose a trade. Nope, just plain ol' grays so far.
Nope, just plain ol' grays so far. Ah, that's a shame. Well, if you find any within the next three days, do let me know. I would be ever so grateful.
Ah, that's a shame. Well, if you find any within the next three days, do let me know. I would be ever so grateful. We'll keep an eye out.
We'll keep an eye out. hi kirj
hi kirjYou should probably hand over the stuff when you get a chance, reader. It'll come in handy when you do, and then much more handy later down the line.


 'Sup.
'Sup. Nice of you to join us, Ace.
Nice of you to join us, Ace. How's the flying thing going?
How's the flying thing going? Quite well so far. How's your hangover, Liege Ace?
Quite well so far. How's your hangover, Liege Ace? Hurting like a real bastard, but I can function.
Hurting like a real bastard, but I can function. Those birds we just caught were gold.
Those birds we just caught were gold. Oh shit, we caught some golden geese? Niiiice.
Oh shit, we caught some golden geese? Niiiice. I wonder if foie gras made from golden geese is expensive.
I wonder if foie gras made from golden geese is expensive. Fwah grah? Is that named after the noise they make?
Fwah grah? Is that named after the noise they make? No. All I know is that the name comes from a dead language.
No. All I know is that the name comes from a dead language. Crazy gibberish.
Crazy gibberish. It's like steak, but it's made from goose liver. Sometimes duck.
It's like steak, but it's made from goose liver. Sometimes duck. Hurk... P-People pay money to eat that?
Hurk... P-People pay money to eat that? A lot of money.
A lot of money. Man, gramma Momoe was right. Rich people really do eat the garbage parts of the food...
Man, gramma Momoe was right. Rich people really do eat the garbage parts of the food...

 That kangaroo is very vigorously shadowboxing at us.
That kangaroo is very vigorously shadowboxing at us. Bounding Beasts will aggro on you if you get close to them, and they can either see you, or you're sufficiently close enough.
Bounding Beasts will aggro on you if you get close to them, and they can either see you, or you're sufficiently close enough.

 Don't eat those carrots.
Don't eat those carrots.
 I believe now would be a good chance to test the foodapult. That chef at the bar did mention that these kangaroos love vegetables.
I believe now would be a good chance to test the foodapult. That chef at the bar did mention that these kangaroos love vegetables.
 Wow, it is beelining for that junk.
Wow, it is beelining for that junk. The foodapult launches food one tile in front of wherever the skyship is facing.
The foodapult launches food one tile in front of wherever the skyship is facing.If an FOE notices dropped food that they like, you'll hear a sound effect play, and hearts will appear over their head. They will then walk towards the food...


 Zero self-preservation instinct, huh.
Zero self-preservation instinct, huh. It's very clearly sick, and yet it keeps eating the poisoned food anyway.
It's very clearly sick, and yet it keeps eating the poisoned food anyway. Even when they're that big, animals are animals.
Even when they're that big, animals are animals. It's a bit hard to see because, well, it's a green particle effect on a green background, but when an FOE eats poisoned food, you can the usual green poison bubble effect floating over their head.
It's a bit hard to see because, well, it's a green particle effect on a green background, but when an FOE eats poisoned food, you can the usual green poison bubble effect floating over their head.Oh, by the way, when you get close to an FOE, you'll get an FOE proximity meter right next to the danger indicator on the bottom-right of the top screen.


 Those must be the soldiers we were asked to deliver food to.
Those must be the soldiers we were asked to deliver food to.

 Don't drop anything too expensive, we need as much money as we can get.
Don't drop anything too expensive, we need as much money as we can get. Tharsis buffalo should be fine.
Tharsis buffalo should be fine.
 Bye, buffalo.
Bye, buffalo. A few minutes later...
A few minutes later... HEY, YOU GUYS!
HEY, YOU GUYS! YEAH?
YEAH? FOOD LOOKS GOOD. YOU CAN GET GOING NOW. THANKS FOR THE HELP!
FOOD LOOKS GOOD. YOU CAN GET GOING NOW. THANKS FOR THE HELP! NO PROBLEM!
NO PROBLEM! The request is now complete! You can turn it in the next time you find yourself at the bar.
The request is now complete! You can turn it in the next time you find yourself at the bar. You can also drop food directly below your ship, in addition to using the foodapult to launch it forward.
You can also drop food directly below your ship, in addition to using the foodapult to launch it forward.

 To the east and west are high mountain ranges, far too tall for your skyship to fly overhead.
To the east and west are high mountain ranges, far too tall for your skyship to fly overhead. ...Hello, everyone. I feel...capable of walking and talking now.
...Hello, everyone. I feel...capable of walking and talking now. Glad to hear it. You haven't missed much.
Glad to hear it. You haven't missed much. Except for the very strong winds coming from that ravine, it seems.
Except for the very strong winds coming from that ravine, it seems. Can't see anything, either. Thickest fog I've ever seen. I'm not going in there, not even a bit.
Can't see anything, either. Thickest fog I've ever seen. I'm not going in there, not even a bit. I find it hard to blame you.
I find it hard to blame you. I wonder what that big hand thing means.
I wonder what that big hand thing means.
 Oh. It probably has something to do with the big hand thing right in front of that labyrinth.
Oh. It probably has something to do with the big hand thing right in front of that labyrinth. You wanna land and scout that place?
You wanna land and scout that place? Mm... No. I wanna finish mapping first.
Mm... No. I wanna finish mapping first. No objections he— Ngh, here...
No objections he— Ngh, here... Not gonna hear me complaining.
Not gonna hear me complaining.

 Those trees look weird.
Those trees look weird. I believe this is the kapok grove the Count wished to know about.
I believe this is the kapok grove the Count wished to know about. I drew an exclamation point here, so we don't forget where the trees are.
I drew an exclamation point here, so we don't forget where the trees are.

 This must be...where the river near Tharsis flows from. What a wonderful chill.
This must be...where the river near Tharsis flows from. What a wonderful chill. Another exclamation point.
Another exclamation point.

 Let's not.
Let's not. I know some captains who're into the whole tornado thing, but it's not for me.
I know some captains who're into the whole tornado thing, but it's not for me. If there weren't a kid around, I'd have a lotta questions.
If there weren't a kid around, I'd have a lotta questions. Flying into a tornado is bad! You'll be sent back to town, you'll lose all of your current food without getting paid for it, all of your current party members will be reduced to 1 HP, and you'll lose some money to pay for repairs.
Flying into a tornado is bad! You'll be sent back to town, you'll lose all of your current food without getting paid for it, all of your current party members will be reduced to 1 HP, and you'll lose some money to pay for repairs.

 There are brightly colored fruits on the trees; many animals seem to flock here to feed on these fruits. You grow excited to think of what manner of exotic beasts you may encounter in this forest.
There are brightly colored fruits on the trees; many animals seem to flock here to feed on these fruits. You grow excited to think of what manner of exotic beasts you may encounter in this forest. Fruit...
Fruit...
 Discovering a cave will allow us to start flying from just outside it, as opposed to starting outside of Tharsis.
Discovering a cave will allow us to start flying from just outside it, as opposed to starting outside of Tharsis.

 You see a stone monument at its entrance that looks clearly man-made. Who built it here, and why? You will never know the answer unless you step into the maze... You steel yourself to begin your explorations.
You see a stone monument at its entrance that looks clearly man-made. Who built it here, and why? You will never know the answer unless you step into the maze... You steel yourself to begin your explorations.
 Barring any major revelations, this should be our primary focus for exploration.
Barring any major revelations, this should be our primary focus for exploration. Map.
Map. After we finish mapping out the plains, yes.
After we finish mapping out the plains, yes.

 Huh, another skyship.
Huh, another skyship. I hope this person is nice, like Kirjonen.
I hope this person is nice, like Kirjonen.
 Hachi-machyes, ma'am.
Hachi-machyes, ma'am. Oh dear. Harper, I believe you should handle this...
Oh dear. Harper, I believe you should handle this... Hi. We're Guild Daffodil, and I'm Harper.
Hi. We're Guild Daffodil, and I'm Harper. So you're the new guild that everyone's talking about.
So you're the new guild that everyone's talking about. If they're talking about Guild Daffodil, then yes. But why are people talking about us?
If they're talking about Guild Daffodil, then yes. But why are people talking about us? You kidding? You took on and cleared the Old Forest Mine trek, all within a few hours.
You kidding? You took on and cleared the Old Forest Mine trek, all within a few hours. What, that not happen much?
What, that not happen much? Pretty much unheard of, least as far as new guilds go.
Pretty much unheard of, least as far as new guilds go. Man, what the hell's wrong with the other—
Man, what the hell's wrong with the other— We're pretty good?
We're pretty good? I'd say so, yeah.
I'd say so, yeah. Yay. Oh, we met another explorer earlier. Kirjonen. They wanted a special fish from us. Do you want anything?
Yay. Oh, we met another explorer earlier. Kirjonen. They wanted a special fish from us. Do you want anything? Now that you mention it... You got any black taurus? I've been dying to have some of that again.
Now that you mention it... You got any black taurus? I've been dying to have some of that again. Mm... No. Sorry.
Mm... No. Sorry. Eh, worth a shot. If you find any in the next few days, lemme know. Good deeds don't go unrewarded!
Eh, worth a shot. If you find any in the next few days, lemme know. Good deeds don't go unrewarded! Thank you, Wiglaf.
Thank you, Wiglaf. Sadly, Wiglaf does not have the sheer muscles she does in her Nexus incarnation.
Sadly, Wiglaf does not have the sheer muscles she does in her Nexus incarnation. literally forgot wiglaf was in nexus until you said this exact message lol
literally forgot wiglaf was in nexus until you said this exact message lol

 Nightfall? Already?
Nightfall? Already? We should probs finish up soon.
We should probs finish up soon. That would be much appreciated, thank you. Harper and I have been awake and taking care of matters since the crack of dawn...
That would be much appreciated, thank you. Harper and I have been awake and taking care of matters since the crack of dawn... Thank you very much for going about town while the rest of us were...incapacitated.
Thank you very much for going about town while the rest of us were...incapacitated. It's no trouble at all, I'm just tired. Yesterday was very much an occasion worth celebrating, so I find it hard to begrudge festive consumption of alcohol.
It's no trouble at all, I'm just tired. Yesterday was very much an occasion worth celebrating, so I find it hard to begrudge festive consumption of alcohol. Patience of a saint.
Patience of a saint. I— Well, I'd like to believe this is simply common courtesy.
I— Well, I'd like to believe this is simply common courtesy. You don't give yourself enough credit, and that's an objective fact.
You don't give yourself enough credit, and that's an objective fact. How?
How? The runes decree it thus.
The runes decree it thus. Do they actually, or are you simply encouraging my ego?
Do they actually, or are you simply encouraging my ego? Yes!
Yes! "Yes" to which one?
"Yes" to which one? Yes.
Yes. ...Right, I have always been told that I need to accept praise more readily, so I'll...accept Shelly's words.
...Right, I have always been told that I need to accept praise more readily, so I'll...accept Shelly's words. That's the spirit!
That's the spirit!

 Its reflection of the surrounding flora is even more beautiful than the real thing, piquing your curiosity. If you could slake your thirst from those clear waters, the exhaustion of your travels would surely vanish.
Its reflection of the surrounding flora is even more beautiful than the real thing, piquing your curiosity. If you could slake your thirst from those clear waters, the exhaustion of your travels would surely vanish.
 Good spot for fresh water... Okay, done.
Good spot for fresh water... Okay, done.

 Huh. A secret passage, but for skyships.
Huh. A secret passage, but for skyships. I wonder what made that hole. Did a kangaroo punch the rock?
I wonder what made that hole. Did a kangaroo punch the rock? ...The fact that I cannot definitely say "no" to that scares me.
...The fact that I cannot definitely say "no" to that scares me.

 Ah, shit. That wasn't supposed to happen.
Ah, shit. That wasn't supposed to happen. Well, what the hell do we do now?
Well, what the hell do we do now? ...Xiaohu, can runes make magic bigger?
...Xiaohu, can runes make magic bigger? Magic is fundamentally just a sequence of runes, so... I would wager yes. What sort of magic are you thinking of, Harper?
Magic is fundamentally just a sequence of runes, so... I would wager yes. What sort of magic are you thinking of, Harper? Thread.
Thread. Thread? I'm unfamiliar with that spell.
Thread? I'm unfamiliar with that spell.
 Ariadne thread.
Ariadne thread. A magic thread, then. What does it do?
A magic thread, then. What does it do? Takes explorers back to a safe place. Can you make it work on the whole ship?
Takes explorers back to a safe place. Can you make it work on the whole ship? Trivially and gladly! Just hold the thread up, and I should be able to invoke an expansion of its power.
Trivially and gladly! Just hold the thread up, and I should be able to invoke an expansion of its power. Ready.
Ready. Ahem... α∞🧵Ω!
Ahem... α∞🧵Ω!

 Wow.
Wow. That... That's impressive.
That... That's impressive. Are there...any limits on what one can do with runic invocations?
Are there...any limits on what one can do with runic invocations? If you know the correct incantations? None whatsoever!
If you know the correct incantations? None whatsoever! Well, that's terrifying.
Well, that's terrifying. It is, isn't it? But it's so very thrilling, too!
It is, isn't it? But it's so very thrilling, too! Mhm. Runes are cool.
Mhm. Runes are cool. Ah, hello, everyone?
Ah, hello, everyone? Hi, Waylon.
Hi, Waylon. Yes, what just happened? I was looking outside my window, observing the kangaroos, and then in an instant, we were back at the city gates.
Yes, what just happened? I was looking outside my window, observing the kangaroos, and then in an instant, we were back at the city gates. I combined a runic invocation with one of Harper's...?
I combined a runic invocation with one of Harper's...? Ariadne threads.
Ariadne threads. Yes, Ariadne threads, to expand its power, and transport the ship to safety.
Yes, Ariadne threads, to expand its power, and transport the ship to safety. I see. Well, actually, no, I don't see, but I'll do my best to try and figure out a way to see.
I see. Well, actually, no, I don't see, but I'll do my best to try and figure out a way to see. It's magic. Big magic.
It's magic. Big magic. Harper does indeed have the long and short of it!
Harper does indeed have the long and short of it! I... I'll take your word for it. In any case, do we have any plans for dinner? It's getting late, and the others were getting hungry.
I... I'll take your word for it. In any case, do we have any plans for dinner? It's getting late, and the others were getting hungry. ...Oh. I forgot to cook. Sorry.
...Oh. I forgot to cook. Sorry. Inn food it is, then.
Inn food it is, then.

 Ack, fuhta— Did we do something?
Ack, fuhta— Did we do something? It was nothing to be ashamed of... You seem to be doing your all to search the small caves that dot these lands.
It was nothing to be ashamed of... You seem to be doing your all to search the small caves that dot these lands. They are?
They are? We found a way to get to the cave with the kangaroos nearby.
We found a way to get to the cave with the kangaroos nearby. Ah, yes, that one. To my knowledge, that's been confounding other guilds for some time. What did you do to find a way in?
Ah, yes, that one. To my knowledge, that's been confounding other guilds for some time. What did you do to find a way in? We dropped food for the kangaroos.
We dropped food for the kangaroos. ...And then?
...And then? That's it.
That's it. Okay, suddenly Ciaran's griping about the guilds in Tharsis being "useless" makes much more sense.
Okay, suddenly Ciaran's griping about the guilds in Tharsis being "useless" makes much more sense. I would not put it quite like the wharfmaster does, but... Well, nonetheless, all of us in this city are grateful for your contributions. The caves have many rare and desirable materials. The more of them you find, the more we shall flourish. I hope that you continue your efforts on our behalf. But now that Dalla has hungry mouths to feed, I should return to my place of work. Perhaps later, Daffodil...
I would not put it quite like the wharfmaster does, but... Well, nonetheless, all of us in this city are grateful for your contributions. The caves have many rare and desirable materials. The more of them you find, the more we shall flourish. I hope that you continue your efforts on our behalf. But now that Dalla has hungry mouths to feed, I should return to my place of work. Perhaps later, Daffodil... Have a good evening, Kirtida.
Have a good evening, Kirtida. After you discover any cave that isn't the Old Forest Mine, the next time you visit the inn, Kirtida will show up and say, well, that, at you.
After you discover any cave that isn't the Old Forest Mine, the next time you visit the inn, Kirtida will show up and say, well, that, at you.If you've somehow not visited the Dancing Peacock yet, she'll introduce herself at the end of her dialogue, and ask that you visit the Dancing Peacock.


 Good evening, Count.
Good evening, Count. Ah, Mister van Houten, good to see you.
Ah, Mister van Houten, good to see you. Y-You know my name?
Y-You know my name? Well, of course. People talk about you, my good man, especially the apprentice down at the atelier.
Well, of course. People talk about you, my good man, especially the apprentice down at the atelier. Of course she does... In any case, I'm here on behalf of my guild—
Of course she does... In any case, I'm here on behalf of my guild— Daffodil, I'm assuming. This wouldn't happen to be news about the kapok grove, would it?
Daffodil, I'm assuming. This wouldn't happen to be news about the kapok grove, would it? Actually, yes, it is. Our guild took to the skies for the first time today, and found the grove.
Actually, yes, it is. Our guild took to the skies for the first time today, and found the grove. Ah, splendid! May I see it on your map?
Ah, splendid! May I see it on your map?

 Right where this exclamation point is drawn, sir.
Right where this exclamation point is drawn, sir. Hmm... Yes, that is the correct sector. I shall have some scouts dispatched at once to verify that the grove is there.
Hmm... Yes, that is the correct sector. I shall have some scouts dispatched at once to verify that the grove is there. You do have to tap the specific tile where the grove is on the touch screen in order to finish the quest.
You do have to tap the specific tile where the grove is on the touch screen in order to finish the quest.
 Shouldn't be too long, don't worry.
Shouldn't be too long, don't worry. Thank you for being considerate of my time.
Thank you for being considerate of my time.
 Excellent.
Excellent. With these new resources, the city will prosper. As its governor, I thank you from the bottom of my heart. I have already contacted the Dancing Peacock. You may return there to report in and collect your reward.
With these new resources, the city will prosper. As its governor, I thank you from the bottom of my heart. I have already contacted the Dancing Peacock. You may return there to report in and collect your reward. One more thing to do before I can eat... Well, good night, sir.
One more thing to do before I can eat... Well, good night, sir. Have a pleasant evening, Mister van Houten.
Have a pleasant evening, Mister van Houten.

 Ah, Waylon! It feels like it's been ages since you last stopped by.
Ah, Waylon! It feels like it's been ages since you last stopped by. I'm here for business on behalf of the Daffodil Guild, unfortunately.
I'm here for business on behalf of the Daffodil Guild, unfortunately. Oh, what a shame.
Oh, what a shame.
 Regarding the request from the soldiers—
Regarding the request from the soldiers— Ah, yes, I received word that they were delivered food. Here is the reward, as agreed.
Ah, yes, I received word that they were delivered food. Here is the reward, as agreed.


 So, I never actually knew this until I looked at the event scripting for this quest, but delivering a rare point standard or rare food to the soldiers actually increases the reward you get from this quest. Delivering a rare point standard food gives you three medicas and 150 EXP per party member, while delivering a rare food gives you four medicas, and 250 EXP per party member.
So, I never actually knew this until I looked at the event scripting for this quest, but delivering a rare point standard or rare food to the soldiers actually increases the reward you get from this quest. Delivering a rare point standard food gives you three medicas and 150 EXP per party member, while delivering a rare food gives you four medicas, and 250 EXP per party member.You can also deliver poisoned food. You get the same rewards as if you delivered a normal point standard food, but Kirtida will mention that the soldiers got really sick after they ate your food.
 i want to pet... margherita...!!!
i want to pet... margherita...!!!

 I'm going to assume the Count sent word that we finished his task, too?
I'm going to assume the Count sent word that we finished his task, too? Ha, how did you guess? Yes, he did. Can you keep a secret, Waylon?
Ha, how did you guess? Yes, he did. Can you keep a secret, Waylon? Sure?
Sure? This is not the first time the Count has requested that a guild find the kapok grove. Any time a new guild is certified and is given a skyship, like clockwork, the Count comes here to post the request again. As he tells it, the hunt for the kapok grove not only encourages new guilds to pry their attention away from the Lush Woodlands, but also helps them learn to navigate the skies better.
This is not the first time the Count has requested that a guild find the kapok grove. Any time a new guild is certified and is given a skyship, like clockwork, the Count comes here to post the request again. As he tells it, the hunt for the kapok grove not only encourages new guilds to pry their attention away from the Lush Woodlands, but also helps them learn to navigate the skies better. ...I can't say I'm surprised to hear that. Don't worry, though, your—well, his?—secret is safe.
...I can't say I'm surprised to hear that. Don't worry, though, your—well, his?—secret is safe. I thank you for your discretion. Here's the reward, by the way. Do drop by again, Waylon.
I thank you for your discretion. Here's the reward, by the way. Do drop by again, Waylon.
 Simple scopes reveal basically every icon on the map—FOEs, treasure chests, shortcuts, etc.—until you move. I don't use them, since I've played this game before, but they're undeniably useful. Too bad the description is severely mistranslated in the English version, and wasn't even corrected in later games.
Simple scopes reveal basically every icon on the map—FOEs, treasure chests, shortcuts, etc.—until you move. I don't use them, since I've played this game before, but they're undeniably useful. Too bad the description is severely mistranslated in the English version, and wasn't even corrected in later games.


 Ah, wonderful.
Ah, wonderful.


 I hadn't actually invested the skill points we received at level 3 yet. No harm done, really, we didn't get into combat after reaching level 3.
I hadn't actually invested the skill points we received at level 3 yet. No harm done, really, we didn't get into combat after reaching level 3.Shelly puts one point each into Electric Link and Vanguard. Electric Link deals a moderate amount of damage, and if an ally lands a hit on the targeted enemy after Shelly uses Electric Link, a second hit will follow, dealing a percentage of the original hit's damage. Note that follow-up attacks from Link skills will still occur even if the initial user is incapacitated for any reason—debilitating ailments, arm binds, reaching 0 HP, none of those will stop follow-up attacks.
There's an important FOE in one of the caves that has a weakness to fire and volt damage. Aside from that, there's no significant weaknesses to any of the three elemental damage types in the 1st Land, so it's hard to go wrong with taking any of the Links right now. Don't try to level all three at once, though, that's going to get you nowhere fast.
Vanguard places a buff on Shelly that increases the damage she deals with physical attacks (this includes composite physical attacks, like the Links), and gives her priority, but also increases the damage she takes from physical attacks. Vanguard is one of two ways to make landsknechts act quickly, the other simply being outfitting them with equipment that has action speed bonuses. Making landsknechts act quickly is not only important for making sure as many party members as possible can take advantage of the bonuses that their class skill offers, but for Links, it's also important that as many party members as possible get a chance to activate follow-up attacks. The latter isn't really a huge deal early on, since Links are limited to one follow-up at the moment, but it will become much more important once we reach the Veteran tier of skills.
For now, I'm going to be sticking with Vanguard for making Shelly speedy, primarily because Vanguard is a fairly strong buff; at max rank, it'll increase Shelly's physical damage by 40%. However, it will fall off later, for reasons that are best explained later.


 Ace puts their two skill points into Auto-Taunt, providing a significant increase to its activation chance.
Ace puts their two skill points into Auto-Taunt, providing a significant increase to its activation chance.

 Now that Harper has Flank Shot, I decided to have her invest in Leg Snipe, more for unlocking Arm Snipe, than anything.
Now that Harper has Flank Shot, I decided to have her invest in Leg Snipe, more for unlocking Arm Snipe, than anything.The Snipe skills are fairly unique. While they do not deal much damage, they have two notable bits of utility; one of them is obvious, the other is hard to discern from the Custom screen. The first is that the Snipes attempt to bind a body part. The second is that the Snipes cannot miss. They do not check for accuracy at all. Even if Harper would've normally had a 0% chance to hit an enemy, the Snipes would still hit them. Beyond the obvious use of "being able to ensure an enemy dies, without any chance of failure," the Snipes also make for excellent counters to a certain handful of enemies that give themselves guaranteed evasion, and who also punish you if you do not manage to hit them while they are in this state.
As for the three bind types: I think a more in-depth discussion is best saved for a specific mechanics overview, but head binds and arm binds are both just generally useful, while leg binds are situationally useful.


 Eine puts a skill point in Recovery, which lowers the TP cost, and another in Healing, which minorly increases the amount it heals.
Eine puts a skill point in Recovery, which lowers the TP cost, and another in Healing, which minorly increases the amount it heals.

 Rather than unlocking and gaining access to Fireball Rune, I instead put Xiaohu's two skill points into Runic Gleam, a self-targeted buff that increases the damage she deals with TEC-based attacks. Honestly, I should've put the points into Lightning Rune, they would've given her a bigger damage increase than two points in Runic Gleam...but, well, it's the opening hours of the game, all of that is extremely marginal. Once Xiaohu starts increasing the TP cost of her attacks, Runic Gleam will become useful not just as a damage increase, but also as a TP saver. Without bothering you with the exact numbers, once Lightning Rune passes level 5, using it three times under the effect of a max-level Runic Gleam is not only a damage-per-turn increase over just using Lightning Rune four times, it also uses less TP.
Rather than unlocking and gaining access to Fireball Rune, I instead put Xiaohu's two skill points into Runic Gleam, a self-targeted buff that increases the damage she deals with TEC-based attacks. Honestly, I should've put the points into Lightning Rune, they would've given her a bigger damage increase than two points in Runic Gleam...but, well, it's the opening hours of the game, all of that is extremely marginal. Once Xiaohu starts increasing the TP cost of her attacks, Runic Gleam will become useful not just as a damage increase, but also as a TP saver. Without bothering you with the exact numbers, once Lightning Rune passes level 5, using it three times under the effect of a max-level Runic Gleam is not only a damage-per-turn increase over just using Lightning Rune four times, it also uses less TP.
 Sorry it took us all day to come here. That sounds bad.
Sorry it took us all day to come here. That sounds bad. Real bad. So, can ya get me two'a dem rat fangs? You can pry em off'a tree rats what live out in da Lush Woodlands. Once ya gottem, just sell em ta me, and dat'll be dat. Oh, an don't worry, the money yas get from sellin' the fangs ain't part of da reward.
Real bad. So, can ya get me two'a dem rat fangs? You can pry em off'a tree rats what live out in da Lush Woodlands. Once ya gottem, just sell em ta me, and dat'll be dat. Oh, an don't worry, the money yas get from sellin' the fangs ain't part of da reward. A simple fetch quest.
A simple fetch quest.
 ...
... Oh. Good morning, Harper. Is something the matter?
Oh. Good morning, Harper. Is something the matter? ...
... Do you...see something, out on the plains?
Do you...see something, out on the plains? Pookas. Two of them.
Pookas. Two of them.


 What happened, did we get hijack— Harper?!
What happened, did we get hijack— Harper?! ...
... You're...piloting?
You're...piloting? Mhm.
Mhm. Why...did you do that?
Why...did you do that? She said saw two...pookas? I'm going to guess that's the thing in front of us.
She said saw two...pookas? I'm going to guess that's the thing in front of us. Pookas are good luck, and also cute.
Pookas are good luck, and also cute. It's just going "pook pook" at us.
It's just going "pook pook" at us.
 ...Never mind, it's floating towards us.
...Never mind, it's floating towards us. Pook!!
Pook!!

 Are we being attacked?!
Are we being attacked?! No, it's just a pook—
No, it's just a pook—

 Ngah!
Ngah!

 Oh.
Oh. ...I was not expecting it to perish from me throwing a butterknife at it.
...I was not expecting it to perish from me throwing a butterknife at it. Bye, red pooka.
Bye, red pooka. I'm...sorry, Harper, I thought we were in danger.
I'm...sorry, Harper, I thought we were in danger. No, it's...it's okay.
No, it's...it's okay. Uh, I don't mean to interrupt, but is that thing turning into dandelion puffs?
Uh, I don't mean to interrupt, but is that thing turning into dandelion puffs?


 Oh! It left a gift for us.
Oh! It left a gift for us. You're not sad any more?
You're not sad any more? No. I wanted to look at it a bit more, but it's okay. Catching a pooka gives you good luck. They don't die, either, they turn into dandelion puffs, and then the puffs turn into more pookas.
No. I wanted to look at it a bit more, but it's okay. Catching a pooka gives you good luck. They don't die, either, they turn into dandelion puffs, and then the puffs turn into more pookas. ...Well, you managed to pilot us towards it without getting us killed, so... Y'know what? If you see any pookas, feel free to do that again. That book it left behind looks valuable.
...Well, you managed to pilot us towards it without getting us killed, so... Y'know what? If you see any pookas, feel free to do that again. That book it left behind looks valuable. Oh! Okay. I'll keep a good eye out for more pookas. Thank you, Shelly. You're not mad?
Oh! Okay. I'll keep a good eye out for more pookas. Thank you, Shelly. You're not mad? I'm confused that you were able to pilot the Air B'n'B, more than anything. I guess that's worth a "good job"?
I'm confused that you were able to pilot the Air B'n'B, more than anything. I guess that's worth a "good job"? Am I the only one worried that these pookas seem to be an unkillable self-propagating species?
Am I the only one worried that these pookas seem to be an unkillable self-propagating species? Why would that worry you? They go "pook pook."
Why would that worry you? They go "pook pook." ...Yeah, they are cute. Don't mind me, I'm just a chronic worrier.
...Yeah, they are cute. Don't mind me, I'm just a chronic worrier.
Red Pooka
| Level: 1 | HP: 1 | STR: 10 | TEC: 10 | VIT: 10 | AGI: 10 | LUC: 10 | DS: 30 |
Damage Vulnerabilities:
Disable Vulnerabilities:
 So! Pookas. They're sort of a replacement for pasarans from EO3. They can be a bit hard to catch, but they can be lured with food, and if you do manage to get into a battle with one, they're beyond trivially easy to kill.
So! Pookas. They're sort of a replacement for pasarans from EO3. They can be a bit hard to catch, but they can be lured with food, and if you do manage to get into a battle with one, they're beyond trivially easy to kill.Your reward for catching them is a stat-increasing book, consumables that permanently increase one of a character's five main stats (STR, TEC, VIT, AGI, LUC) by one point. These return from EO3, but with a very large nerf: a character can only have ten of a given type of stat book used on them. Ever. Once you've used ten power books on someone, they can no longer be given any more. This was done to fix an exploit in EO3 where, given enough time, one could farm up enough stat books to bring a character to 99 in any stat, or even all of their stats, another way in which you can demolish the idea of class identity in that game.
Each time you kill a pooka, the game rolls a random number of steps, from 650 to 800, that you will have to take before that pooka can spawn again on the overworld. If you, for some inexplicable reason, run away from a pooka battle, or a pooka escapes from the overworld before you can catch it, which is less inexplicable, the game rolls between 325 and 400 steps instead.


 It was at this point that I remembered that I needed to check the Old Forest Mine in order to be able to visit it again. We will actually be coming back here much later in the game!
It was at this point that I remembered that I needed to check the Old Forest Mine in order to be able to visit it again. We will actually be coming back here much later in the game!

 I also managed to catch a sakura trout, the food that Kirjonen wanted.
I also managed to catch a sakura trout, the food that Kirjonen wanted. Liege Kirjonen! We managed to find a sakura trout, as you requested.
Liege Kirjonen! We managed to find a sakura trout, as you requested. Ah, wonderful. I am grateful for your hospitality, Guild Daffodil. Thanks to you, I can fulfill my obligation to the Count. Here, please take this bronze icon. It would please me if you found a use for it in your travels.
Ah, wonderful. I am grateful for your hospitality, Guild Daffodil. Thanks to you, I can fulfill my obligation to the Count. Here, please take this bronze icon. It would please me if you found a use for it in your travels.
 Many thanks.
Many thanks. Kirjonen quietly bows to you and starts up their skyship. You see them off before resuming your own journey.
Kirjonen quietly bows to you and starts up their skyship. You see them off before resuming your own journey.
 The first time you give Kirjonen or Wiglaf the food they request in a given land, they will reward you with a unique accessory. Our reward for bringing Kirjonen their requested food in the 1st Land is this bronze icon. +1 to all stats is nice, but +20 HP is the real prize here, that's a pretty significant amount of HP this early on.
The first time you give Kirjonen or Wiglaf the food they request in a given land, they will reward you with a unique accessory. Our reward for bringing Kirjonen their requested food in the 1st Land is this bronze icon. +1 to all stats is nice, but +20 HP is the real prize here, that's a pretty significant amount of HP this early on. the real prize is that kirj won't dip
the real prize is that kirj won't dip
 While it does mean I have to take off their boots, Ace is a natural fit for the bronze icon, since +20 HP lets them tank a few more hits in a given battle.
While it does mean I have to take off their boots, Ace is a natural fit for the bronze icon, since +20 HP lets them tank a few more hits in a given battle.
 ...And that's the story of what happened earlier.
...And that's the story of what happened earlier. Had yourselves a li'l gay 'n hearty, eh?
Had yourselves a li'l gay 'n hearty, eh? Yes.
Yes. You understood that?
You understood that? I understand what all of those words mean.
I understand what all of those words mean. Did anyone actually, oh, read the book yet?
Did anyone actually, oh, read the book yet? I did. The first page was blank. When I turned the page over, the book disappeared, and I felt a little stronger.
I did. The first page was blank. When I turned the page over, the book disappeared, and I felt a little stronger. I was not expecting our village's artifacts to turn up on the outside...
I was not expecting our village's artifacts to turn up on the outside... Wait, you know about these things?
Wait, you know about these things? We had a large stockpile of these books. Where they came from is, unfortunately, a story buried beneath the sands of time. Exemplary deeds are to be rewarded with an increase in one's natural abilities—provided by the book, of course. I was fortunate enough to be able to partake of one when I was a child.
We had a large stockpile of these books. Where they came from is, unfortunately, a story buried beneath the sands of time. Exemplary deeds are to be rewarded with an increase in one's natural abilities—provided by the book, of course. I was fortunate enough to be able to partake of one when I was a child.


 Anyone got anything else they wanna take care of?
Anyone got anything else they wanna take care of? Nah.
Nah. No.
No. I finished mapping, so no.
I finished mapping, so no. I am quite ready to venture into a labyrinth again!
I am quite ready to venture into a labyrinth again! Alright. Lush Woodlands time it is, then.
Alright. Lush Woodlands time it is, then. I'll bring the ship back around to the city gates. Be safe and be brave, you five.
I'll bring the ship back around to the city gates. Be safe and be brave, you five. Kick some arses out there for me!
Kick some arses out there for me! Okay.
Okay.



 The foliage is even denser than it was in the Old Forest Mine.
The foliage is even denser than it was in the Old Forest Mine. Man, did it get really humid soon as we stepped in here?
Man, did it get really humid soon as we stepped in here? I suspect these labyrinths have highly-localized environs and weather, possibly owing to—as Eine mentioned—the unique trees that surround us, though that is merely speculation. It's entirely possible that the trees cause the highly-localized environs!
I suspect these labyrinths have highly-localized environs and weather, possibly owing to—as Eine mentioned—the unique trees that surround us, though that is merely speculation. It's entirely possible that the trees cause the highly-localized environs! That was a lot more scientific and specific than I was expecting.
That was a lot more scientific and specific than I was expecting. You'd be quite surprised what even just a cursory runic examination can reveal about...well, anything! Meri and I made several discoveries about the toxins her family employs while we were travelling to Tharsis.
You'd be quite surprised what even just a cursory runic examination can reveal about...well, anything! Meri and I made several discoveries about the toxins her family employs while we were travelling to Tharsis.

 The beautiful scenery has a pleasant breeze that passes through, rustling the grass and the trees. Yet despite the soothing atmosphere, you have not forgotten that this place has claimed countless lives. You resolve to test your mettle against the labyrinthine hazards once more...
The beautiful scenery has a pleasant breeze that passes through, rustling the grass and the trees. Yet despite the soothing atmosphere, you have not forgotten that this place has claimed countless lives. You resolve to test your mettle against the labyrinthine hazards once more... The game provides a tutorial on the autopilot system here, for some reason. You can use specific icons to draw a path that your party will automatically follow after pressing the giant play button on the right there. I don't use it at all, in no small part because the tools for constructing autopilot paths in EO4 are very immature, especially when compared to the version introduced in EO2U.
The game provides a tutorial on the autopilot system here, for some reason. You can use specific icons to draw a path that your party will automatically follow after pressing the giant play button on the right there. I don't use it at all, in no small part because the tools for constructing autopilot paths in EO4 are very immature, especially when compared to the version introduced in EO2U.

 That's the light pillar the Count talked about. Let's go look.
That's the light pillar the Count talked about. Let's go look.

 As you gaze upon it, a nearby soldier addresses you.
As you gaze upon it, a nearby soldier addresses you.
 You touch it, and you'll be able to go to and fro between the city and the forest in an eyeblink.
You touch it, and you'll be able to go to and fro between the city and the forest in an eyeblink. Oh, handy, an easy way out and in.
Oh, handy, an easy way out and in. Do you know how it—
Do you know how it— No, I don't. Don't bother asking around how it works. It was here when other explorers found this maze long ago. But it's handy, that you can be sure of. My advice? Put it to use, and never you mind the particulars.
No, I don't. Don't bother asking around how it works. It was here when other explorers found this maze long ago. But it's handy, that you can be sure of. My advice? Put it to use, and never you mind the particulars. Having finished talking, the soldier leaves his place, seeming pleased with himself... You are left free to test out the Geomagnetic Pole or to continue your wanderings.
Having finished talking, the soldier leaves his place, seeming pleased with himself... You are left free to test out the Geomagnetic Pole or to continue your wanderings.  Do the runes say anything about the pole? Did someone make it and put it here?
Do the runes say anything about the pole? Did someone make it and put it here? ...Its history is inscrutable, sadly.
...Its history is inscrutable, sadly. Oh well.
Oh well.

 Interacting with the geomagnetic pole immediately places it on our map. It also, silently, unlocks the ability for us to immediately warp to it from the city gates, meaning we don't have to take the skyship to the Lush Woodlands' place on the Windy Plains every time we wish to visit it. I'll still be doing that, though, so I can take advantage of food buffs.
Interacting with the geomagnetic pole immediately places it on our map. It also, silently, unlocks the ability for us to immediately warp to it from the city gates, meaning we don't have to take the skyship to the Lush Woodlands' place on the Windy Plains every time we wish to visit it. I'll still be doing that, though, so I can take advantage of food buffs.


 More of the armadillos and grasshoppers. But... Is that a bipdeal rat?
More of the armadillos and grasshoppers. But... Is that a bipdeal rat? Yep. It's huge, too.
Yep. It's huge, too. With even huger teeth.
With even huger teeth.
Tree Rat
| Level: 3 | HP: 61 | STR: 10 | TEC: 8 | VIT: 6 | AGI: 10 | LUC: 7 | DS: 22 |
Damage Vulnerabilities:
Disable Vulnerabilities:
 Deadly Incisor: Deals heavy cut damage to one party member. Fast.
Deadly Incisor: Deals heavy cut damage to one party member. Fast.
 Deadly Incisor: Deals 180% melee STR-based cut damage to one party member. Has a speed modifier of +5, and a base accuracy of 99%.
Deadly Incisor: Deals 180% melee STR-based cut damage to one party member. Has a speed modifier of +5, and a base accuracy of 99%.
- If a Tree Rat began the battle in the back row, once they move to the front row, they will do nothing but spam Deadly Incisor.
- Otherwise, Tree Rats only begin using Deadly Incisor once they're below 50% HP.
- If the Tree Rat is in the back row:
- Attack.
- If the Tree Rat has been in the back row at any point in the battle:
- Use Deadly Incisor.
- If the Tree Rat's HP is below 50%:
- 80% chance to use Deadly Incisor.
- 20% chance to ttack.
- If none of the above occurred:
- Attack.
Drops:
 Rat Fang: 70% chance. Sells for 5 en.
Rat Fang: 70% chance. Sells for 5 en. Kopis (27 ATK, 2 Slots): Made from
Kopis (27 ATK, 2 Slots): Made from 2 Rat Fangs . Costs 180 en. Rat Hide: 50% chance. Sells for 7 en.
Rat Hide: 50% chance. Sells for 7 en. Beast Bow (23 ATK, 1 Slot): Made from
Beast Bow (23 ATK, 1 Slot): Made from 1 Baboon Bone (Angry Baboon Drop) and1 Rat Hide . Costs 170 en. Hide Aspis (10 DEF): Made from
Hide Aspis (10 DEF): Made from 2 Rat Hides . Costs 230 en.
 Rats, I think, ought to stay their regular size. I have worries as to how human societies might manage if pests of the size that Tharsis boasts were to come to the Empire—rats are carnivores, after all. These don't seem to be particularly different from regular-sized rats, mind you—they're just large.
Rats, I think, ought to stay their regular size. I have worries as to how human societies might manage if pests of the size that Tharsis boasts were to come to the Empire—rats are carnivores, after all. These don't seem to be particularly different from regular-sized rats, mind you—they're just large. There's not much to tree rats, really, other than dealing noticeably more damage than both rollers and grasseaters. Early enemies are rarely interesting.
There's not much to tree rats, really, other than dealing noticeably more damage than both rollers and grasseaters. Early enemies are rarely interesting.

 Sonuvva— It's all the way back there, and it still hurt more than the rollers!
Sonuvva— It's all the way back there, and it still hurt more than the rollers!

 Agh! Okay, you wanna go, you fuckin' rodent?
Agh! Okay, you wanna go, you fuckin' rodent?

 That's for biting me.
That's for biting me.

 Ah, hell, I'm already talking to the animals again.
Ah, hell, I'm already talking to the animals again. Is that a bad thing?
Is that a bad thing? Didn't get very far, but I did get to explore a bit of Armoroad's labyrinth. The people I went with gave me weird looks when I started trash-talking the stuff we were fighting.
Didn't get very far, but I did get to explore a bit of Armoroad's labyrinth. The people I went with gave me weird looks when I started trash-talking the stuff we were fighting. That doesn't sound like a bad thing.
That doesn't sound like a bad thing. I mean, I guess? I dunno, it's...kinda more impulsive than anything. I dunno why I do it, it's not like the things are gonna talk back.
I mean, I guess? I dunno, it's...kinda more impulsive than anything. I dunno why I do it, it's not like the things are gonna talk back. You're far from the only person who thinks out loud, or talks to things that are incapable of responding.
You're far from the only person who thinks out loud, or talks to things that are incapable of responding. Meri greatly enjoys talking to cats, for example!
Meri greatly enjoys talking to cats, for example! ...Still feel a bit weird, but thanks, guys.
...Still feel a bit weird, but thanks, guys.


 Do let me treat your wounds before we continue, however.
Do let me treat your wounds before we continue, however. Oh, right, probably a good AAAAAAAGH THAT STINGS!
Oh, right, probably a good AAAAAAAGH THAT STINGS! Yes, sorry, I should have warned you. The stinging liquid is disinfectant, it will prevent your wounds from being infected. Free access to your blood is something that the microorganisms that cause disease would love to take advantage of—the disinfectant will help keep them out.
Yes, sorry, I should have warned you. The stinging liquid is disinfectant, it will prevent your wounds from being infected. Free access to your blood is something that the microorganisms that cause disease would love to take advantage of—the disinfectant will help keep them out. That's... That's all good, I guess, but I don't think you get how much that stung.
That's... That's all good, I guess, but I don't think you get how much that stung. I would direct your attention to the bandage on my left cheek.
I would direct your attention to the bandage on my left cheek. Oh, that's what that is?
Oh, that's what that is? ...I don't know what you could've thought it was besides a bandage, but nevertheless, I do remember the stinging, if that is of any comfort to you.
...I don't know what you could've thought it was besides a bandage, but nevertheless, I do remember the stinging, if that is of any comfort to you.

 That is a very overpowering smell. What could be causing that?
That is a very overpowering smell. What could be causing that? There's a large amount of sap oozing from these fallen trees. I would venture the smell is coming from said sap.
There's a large amount of sap oozing from these fallen trees. I would venture the smell is coming from said sap. Aw. That's not the right kind of sap for making syrup.
Aw. That's not the right kind of sap for making syrup. Much as it hurts to admit, I don't think I'm gonna be able to cut through these. All that'd probably do is make my sword sticky.
Much as it hurts to admit, I don't think I'm gonna be able to cut through these. All that'd probably do is make my sword sticky. I'd bet good money the sap'll attract monsters if we stay too long. Let's get a move on.
I'd bet good money the sap'll attract monsters if we stay too long. Let's get a move on.



 ...What, you're not gonna crack a pun? "A piercing cold" is right there.
...What, you're not gonna crack a pun? "A piercing cold" is right there. What is a "pun?"
What is a "pun?"


 Ah, look over there! That flora looks useful...
Ah, look over there! That flora looks useful...
- Gathers Per Day: 3
 Forest Aloe: 80% chance. Sells for 20 en.
Forest Aloe: 80% chance. Sells for 20 en. Theriaca B: Made from
Theriaca B: Made from 1 Forest Aloe . Costs 90 en. Small Flower: 20% chance. Sells for 45 en.
Small Flower: 20% chance. Sells for 45 en. Nectar: Made from
Nectar: Made from 1 Small Flower . Costs 200 en.
Received  forest aloe x3.
forest aloe x3.
 Gathering mechanics are extraordinarily simple in EO4. I didn't bring it up in the Old Forest Mine, since that was scripted to play out a certain way, but every time you gather something, it's a simple RNG roll to determine what item you get from that point.
Gathering mechanics are extraordinarily simple in EO4. I didn't bring it up in the Old Forest Mine, since that was scripted to play out a certain way, but every time you gather something, it's a simple RNG roll to determine what item you get from that point.If you have any party members who know the gathering skill associated with the gathering point—Herbology for take points, Dendrology for chop points, and Mineralogy for mine points—then they have a 10% chance, any time you gather from one of those points, to find that point's rare item. This is done independently of the actual gather roll.


 ...I've got an idea. Xiaohu, soon as I throw my sword at the trees, throw some lightning at it.
...I've got an idea. Xiaohu, soon as I throw my sword at the trees, throw some lightning at it. Are you planning on using an explosion to clear the way for a shortcut?
Are you planning on using an explosion to clear the way for a shortcut? Bingo.
Bingo. I can hardly say no to an opportunity to be useful!
I can hardly say no to an opportunity to be useful! Alright, now!
Alright, now! α▬⚡Ω!
α▬⚡Ω!

 Thank you, Shelly. How are you gonna fight without a sword, though? Are you gonna punch the enemies?
Thank you, Shelly. How are you gonna fight without a sword, though? Are you gonna punch the enemies? Nah, never was any good at that. I just carry around a bunch more swords in my pack.
Nah, never was any good at that. I just carry around a bunch more swords in my pack. Are all of them coated in explosive chemicals...?
Are all of them coated in explosive chemicals...? Nah.
Nah. Oh, thank the—
Oh, thank the— Not yet, anyways. I keep the boom juice in a different pocket.
Not yet, anyways. I keep the boom juice in a different pocket. ...I-I see.
...I-I see.

 Oh, we've got the rat teeth that Wynne wanted. Yay.
Oh, we've got the rat teeth that Wynne wanted. Yay.

 —! Behind me!
—! Behind me!


 Oh! That one on the right is special...
Oh! That one on the right is special... It looks like a simple roller to me.
It looks like a simple roller to me. Me too.
Me too. Same.
Same. ...Nah, Xiaohu's right. Something's not right with it. I don't like that look in its eyes.
...Nah, Xiaohu's right. Something's not right with it. I don't like that look in its eyes. Rare breed monsters are a new mechanic introduced in EO4. Normal enemies and FOEs both have a small chance, ranging from 2% to 5% for normal enemies and 5% to 10% for FOEs, of spawning as rare breeds.
Rare breed monsters are a new mechanic introduced in EO4. Normal enemies and FOEs both have a small chance, ranging from 2% to 5% for normal enemies and 5% to 10% for FOEs, of spawning as rare breeds.

 Tch, speedy little prick, huh?
Tch, speedy little prick, huh? Rare breeds are extremely fast—they have a flat 10x multiplier applied to their action speed—and deal increased damage. Every time a rare breed enemy glows, their damage output increases by 20%. In almost every case, this means that for every turn that passes, they gain an additional 20% damage, but there are the occasional edge cases where you can prevent them from glowing, so it's probably best to make things as clear as possible.
Rare breeds are extremely fast—they have a flat 10x multiplier applied to their action speed—and deal increased damage. Every time a rare breed enemy glows, their damage output increases by 20%. In almost every case, this means that for every turn that passes, they gain an additional 20% damage, but there are the occasional edge cases where you can prevent them from glowing, so it's probably best to make things as clear as possible.When a normal monster is a rare breed, the first thing it checks for is if it should escape. Much like their damage, a rare breed monster's chance of escaping from battle increases. You can keep them from running by binding their legs, if you want to. Rare breed FOEs do not attempt to escape from battle.


 I dunno, you two, it just seemed like a normal roller to me. Died just as easy as any of them.
I dunno, you two, it just seemed like a normal roller to me. Died just as easy as any of them. Did you not see how quickly that thing rushed me?
Did you not see how quickly that thing rushed me?



 Well, whatever.
Well, whatever. I am surprised you were able to perceive that roller's golden glow.
I am surprised you were able to perceive that roller's golden glow. Huh? Nah, I didn't see anything like that, it was just... Man, I dunno, I said it was the look in its eyes, but it's really hard to describe.
Huh? Nah, I didn't see anything like that, it was just... Man, I dunno, I said it was the look in its eyes, but it's really hard to describe. Fascinating. Well, try not to let the fact that the others could not see it bother you too much.
Fascinating. Well, try not to let the fact that the others could not see it bother you too much. ...Right. I'll try.
...Right. I'll try. Your reward for defeating rare breeds is increased EXP. Rare breeds give out 5x the monster's normal EXP.
Your reward for defeating rare breeds is increased EXP. Rare breeds give out 5x the monster's normal EXP. For a full party this means that each character actually gets the monster's base EXP yields. Math is funny sometimes.
For a full party this means that each character actually gets the monster's base EXP yields. Math is funny sometimes.


 Butterflies with wings bigger than my hand. Huh.
Butterflies with wings bigger than my hand. Huh. At the very least, being an explorer does not leave one wanting for peculiarities.
At the very least, being an explorer does not leave one wanting for peculiarities.
Woodfly
| Level: 4 | HP: 68 | STR: 6 | TEC: 10 | VIT: 4 | AGI: 9 | LUC: 12 | DS: 34 |
Damage Vulnerabilities:
Disable Vulnerabilities:
 Flashy Scales: Attempts to inflict blind on one party member, with a very high chance. Fast.
Flashy Scales: Attempts to inflict blind on one party member, with a very high chance. Fast.
 Flashy Scales: Attempts to inflict blind on one party member, with a 70% base chance. Has a speed modifier of +5.
Flashy Scales: Attempts to inflict blind on one party member, with a 70% base chance. Has a speed modifier of +5.
- Woodflies are very likely to use Flashy Scales on the first turn.
- After the first turn, Woodflies still prefer using Flashy Scales over normal attacks.
- If this is the first turn:
- 80% chance to use Flashy Scales.
- 20% chance to attack.
- If all player characters are afflicted with blind:
- Attack.
- If none of the above occurred:
- 60% chance to use Flashy Scales.
- 40% chance to attack.
Drops:
 Gritty Scales: 70% chance. Sells for 5 en.
Gritty Scales: 70% chance. Sells for 5 en. Balisong (37 ATK, 12% Poison Imbue): Made from
Balisong (37 ATK, 12% Poison Imbue): Made from 1 Writhing Bulb (Fanged Vine Drop 2) and1 Gritty Scales . Costs 560 en. Blind Gas: Made from
Blind Gas: Made from 2 Gritty Scales . Costs 150 en. Thin Wing: 50% chance. Sells for 7 en.
Thin Wing: 50% chance. Sells for 7 en. Scale Mail (26 DEF): Made from
Scale Mail (26 DEF): Made from 1 Roller Shell (Roller Drop 2) and1 Thin Wing . Costs 390 en. Chemise (20 DEF): Made from
Chemise (20 DEF): Made from 1 Fawn Hide (Furyfawn Drop 1) and1 Thin Wing . Costs 220 en.
 I find myself lucky that I wear glasses—it makes it difficult for woodflies to blind me with their scales. This breed is bothersome—their scales are inflicted with a potent, though quite temporary, toxin that specifically clouds over the eyes with a bright light to debilitate prey. Their wings, however, are quite weak to thrusting—the stab of a rapier or a bow, for instance, will shatter in their wings and cause those scales to afflict the woodfly itself. Always a good idea to keep something sharp and pointy about, even if just a dart or something.
I find myself lucky that I wear glasses—it makes it difficult for woodflies to blind me with their scales. This breed is bothersome—their scales are inflicted with a potent, though quite temporary, toxin that specifically clouds over the eyes with a bright light to debilitate prey. Their wings, however, are quite weak to thrusting—the stab of a rapier or a bow, for instance, will shatter in their wings and cause those scales to afflict the woodfly itself. Always a good idea to keep something sharp and pointy about, even if just a dart or something. Neat, our first enemy that can inflict a disable. Woodflies aren't dangerous on their own, they just prolong battles—which can be dangerous if a different enemy can, say, deal a lot of physical damage. Blind multiplies a character's accuracy by 0.33x, applied after almost all of the accuracy formula, but before HIT forges are taken into account. That'll make sense later, don't worry.
Neat, our first enemy that can inflict a disable. Woodflies aren't dangerous on their own, they just prolong battles—which can be dangerous if a different enemy can, say, deal a lot of physical damage. Blind multiplies a character's accuracy by 0.33x, applied after almost all of the accuracy formula, but before HIT forges are taken into account. That'll make sense later, don't worry.They also introduce a series tradition: winged enemies having a weakness to stab damage. I don't really have a good reason for why that is, other than "people hunt flying things with bows and guns."


 Ow.
Ow. You alright there?
You alright there? Mhm. Shooting a bunch of arrows really fast just hurts my wrist.
Mhm. Shooting a bunch of arrows really fast just hurts my wrist.

 Agh, that light is blinding! I can't see!
Agh, that light is blinding! I can't see!

 Skewered woodfly, anyone?
Skewered woodfly, anyone?

 Those wouldn't give much meat, you'd need a lot of dead woodflies to actually make something you could really eat. The wings would make for a good garnish, though.
Those wouldn't give much meat, you'd need a lot of dead woodflies to actually make something you could really eat. The wings would make for a good garnish, though. The fact that you could create a meal from these monsters, even if it does require a large amount of them, is simply astonishing to me.
The fact that you could create a meal from these monsters, even if it does require a large amount of them, is simply astonishing to me. Monster cuisine is all about making sure absolutely nothing an explorer can take goes to waste. Miss Regina Dubois and my uncle Ranger helped pioneer the art back in High Lagaard. I haven't gotten to cook much monster cuisine, though. Most of the monsters you can find in the upper parts of Armoroad's Yggdrasil don't make for very good food. Especially the big walking durians.
Monster cuisine is all about making sure absolutely nothing an explorer can take goes to waste. Miss Regina Dubois and my uncle Ranger helped pioneer the art back in High Lagaard. I haven't gotten to cook much monster cuisine, though. Most of the monsters you can find in the upper parts of Armoroad's Yggdrasil don't make for very good food. Especially the big walking durians.

 ...
... She's not lying. Lemme tell ya, fighting one of those durians ain't fun, between the thorns in your eyes, and the stench.
She's not lying. Lemme tell ya, fighting one of those durians ain't fun, between the thorns in your eyes, and the stench. I am quite glad that things have been smooth sailing for us, so far.
I am quite glad that things have been smooth sailing for us, so far. Oh, and the fuckin' lynxes, don't get me started on those.
Oh, and the fuckin' lynxes, don't get me started on those.


 Careful, there's a bunch of splinters here. Uneven ground.
Careful, there's a bunch of splinters here. Uneven ground. Hm. These are the same trees we saw earlier. The sap smell is the same.
Hm. These are the same trees we saw earlier. The sap smell is the same.

 Least all these trees blocking us make deciding where to go pretty easy.
Least all these trees blocking us make deciding where to go pretty easy.♪ No music ♪


 That's not a good noise.
That's not a good noise.



 That bear seems...very capable of pounding us into jelly...
That bear seems...very capable of pounding us into jelly... Pounding us? I'm more scared of those claws!
Pounding us? I'm more scared of those claws! The kangaroos pursued us too, but this feels significantly scarier...!
The kangaroos pursued us too, but this feels significantly scarier...! Those legs are really short.
Those legs are really short. ...Heh. It's fine. We'll be fine.
...Heh. It's fine. We'll be fine.


 Ace— Hey, where are you going?!
Ace— Hey, where are you going?! C'mon, follow me. I've got an idea.
C'mon, follow me. I've got an idea.



 Dumbass. See, I told you we'd be fine. Stupid bears can't resist the smell of sap.
Dumbass. See, I told you we'd be fine. Stupid bears can't resist the smell of sap. You are rather blasé about this massive FOE hunting us—
You are rather blasé about this massive FOE hunting us— C'mon, Eine, it's fine.
C'mon, Eine, it's fine.


 We're busy, woodflies.
We're busy, woodflies. Nah, we're not. We've got time.
Nah, we're not. We've got time.

 Oh, nice.
Oh, nice.





 Since everyone can actually function in combat now, at least to a degree, I invest their skill points in their gathering skills.
Since everyone can actually function in combat now, at least to a degree, I invest their skill points in their gathering skills.



 Hey, how about that, the bear opened up some paths for us.
Hey, how about that, the bear opened up some paths for us. Ace, I don't think you're okay.
Ace, I don't think you're okay. What're you talking about? I'm fine. Nothing's wrong.
What're you talking about? I'm fine. Nothing's wrong.

 ...Is the bear guarding that patch of aloe and flowers?
...Is the bear guarding that patch of aloe and flowers?

 I dunno, but we're kind of cornered now!
I dunno, but we're kind of cornered now! ...Not quite. Harper, please fire as strong a shot as you can muster, directly ahead.
...Not quite. Harper, please fire as strong a shot as you can muster, directly ahead. ...
...

 Was that okay?
Was that okay? Indeed! We appear to be safe.
Indeed! We appear to be safe. Yeah, I think the bear's stopped chasing us.
Yeah, I think the bear's stopped chasing us. Do you need us to go back to town? You really didn't sound in your right mind there.
Do you need us to go back to town? You really didn't sound in your right mind there. I'm serious, Shelly. I'm fine.
I'm serious, Shelly. I'm fine. ...Alright, I'll trust you. No shame in going back to town once things get to be too much, though, understood? That goes for everyone.
...Alright, I'll trust you. No shame in going back to town once things get to be too much, though, understood? That goes for everyone. On another note, my gods, but is that a foul stench.
On another note, my gods, but is that a foul stench. Wasn't gonna mention it after we got chased, but yeah, what the hell is that?
Wasn't gonna mention it after we got chased, but yeah, what the hell is that?

 It's not coming from this chest. All it had was a knife.
It's not coming from this chest. All it had was a knife.

 Huh. Y'know, I think I could actually use this!
Huh. Y'know, I think I could actually use this! The main gauche is one of a handful of weapons that are not made from monster drops, you just find them in the labyrinth, or from quests. +3 VIT's not bad at all for Ace, so I have her equip it.
The main gauche is one of a handful of weapons that are not made from monster drops, you just find them in the labyrinth, or from quests. +3 VIT's not bad at all for Ace, so I have her equip it.

 Urgh... I don't know what those plants are, but judging on the odor alone, we should leave them alone...
Urgh... I don't know what those plants are, but judging on the odor alone, we should leave them alone... This particular take point is very important! We will be back here later.
This particular take point is very important! We will be back here later.

 Until then, the only thing this point will give us is forest aloe.
Until then, the only thing this point will give us is forest aloe.

 Ah, marvelous! One of these finally survived being picked.
Ah, marvelous! One of these finally survived being picked. What's so special about that flower?
What's so special about that flower? It can be used to make an incredibly revitalizing medicine, said to be able to bring one back from the deepest exhaustion, or even the brink of death.
It can be used to make an incredibly revitalizing medicine, said to be able to bring one back from the deepest exhaustion, or even the brink of death. Nectar.
Nectar. Yes, exactly.
Yes, exactly.- Gathers Per Day: 4
 Forest Aloe: 70% chance. Sells for 20 en.
Forest Aloe: 70% chance. Sells for 20 en. Theriaca B: Made from
Theriaca B: Made from 1 Forest Aloe . Costs 90 en. Small Flower: 30% chance. Sells for 45 en.
Small Flower: 30% chance. Sells for 45 en. Nectar: Made from
Nectar: Made from 1 Small Flower . Costs 200 en.
Received  forest aloe x2, and
forest aloe x2, and  small flower x2.
small flower x2.
 You've got slightly better odds of getting small flowers from this point than the one near the entrance, though not much better.
You've got slightly better odds of getting small flowers from this point than the one near the entrance, though not much better.

 Alright, Xiaohu, what elaborate measure must we undertake in order to pass through here?
Alright, Xiaohu, what elaborate measure must we undertake in order to pass through here? Hmm... Ah, yes, I see! Shelly, Ace, if you would cut through the brush here?
Hmm... Ah, yes, I see! Shelly, Ace, if you would cut through the brush here? On it.
On it. Gotcha.
Gotcha.

 ...That's it. Hm.
...That's it. Hm. Were you expecting something more?
Were you expecting something more?

 "Those who have, should share their bounty. Those who lack, take what you need with gratitude."
"Those who have, should share their bounty. Those who lack, take what you need with gratitude." Gonna guess people leave useful stuff here so that new explorers can have an easier time of things.
Gonna guess people leave useful stuff here so that new explorers can have an easier time of things. Well, we're certainly off to a good start, as far as I can ascertain. Why don't we partake in some charity?
Well, we're certainly off to a good start, as far as I can ascertain. Why don't we partake in some charity?
 I'll leave a thread.
I'll leave a thread. Good thing you carry two, eh?
Good thing you carry two, eh? Who can say? It may save some future explorer's life. You return to your journey with a spring in your step.
Who can say? It may save some future explorer's life. You return to your journey with a spring in your step. Don't feel pressured to leave a nectar here, if you have one. Leaving either it or an Ariadne thread will have the same result later on.
Don't feel pressured to leave a nectar here, if you have one. Leaving either it or an Ariadne thread will have the same result later on.Don't leave the leaves, though. Beyond that being just an unkind and inconsiderate thing to do, you'll miss out on a reward later.




 —!
—! It's one of those baboons the hunter warned us about!
It's one of those baboons the hunter warned us about! Was it trying to ambush us at the charity box?
Was it trying to ambush us at the charity box? Heh, crafty bastard.
Heh, crafty bastard.
Angry Baboon
| Level: 7 | HP: 182 | STR: 15 | TEC: 10 | VIT: 11 | AGI: 11 | LUC: 7 | DS: 24 |
Damage Vulnerabilities:
Disable Vulnerabilities:
 Swing: Deals severe cut damage to one party member.
Swing: Deals severe cut damage to one party member. Throw: Requires a Roller to use. Deals heavy ranged bash damage to one row of party members. The Roller takes damage after use. Fast.
Throw: Requires a Roller to use. Deals heavy ranged bash damage to one row of party members. The Roller takes damage after use. Fast. Throw: Require a Big Roller to use. Deals heavy ranged bash damage to all party members. Fast.
Throw: Require a Big Roller to use. Deals heavy ranged bash damage to all party members. Fast.
 Swing: Deals 150% melee STR-based cut damage to one party member. Has a speed modifier of ±0, and a base accuracy of 99%.
Swing: Deals 150% melee STR-based cut damage to one party member. Has a speed modifier of ±0, and a base accuracy of 99%. Throw: Requires a Roller to use. Deals 100% ranged STR-based bash damage to one row of party members. Enemies that participate in using this skill suffer 100% melee STR-based bash damage. Has a speed modifier of +5, and a base accuracy of 99%.
Throw: Requires a Roller to use. Deals 100% ranged STR-based bash damage to one row of party members. Enemies that participate in using this skill suffer 100% melee STR-based bash damage. Has a speed modifier of +5, and a base accuracy of 99%. Throw: Require a Big Roller to use. Deals 130% ranged STR-based bash damage to all party members. Has a speed modifier of +5, and a base accuracy of 99%.
Throw: Require a Big Roller to use. Deals 130% ranged STR-based bash damage to all party members. Has a speed modifier of +5, and a base accuracy of 99%.
- Angry Baboons are unlikely to use Swing when the party is blindsided.
- Angry Baboons become far more likely to use Swing when at low HP.
- Angry Baboons are very likely to use Throw if a Roller or Big Roller is in the battle.
- After using either version of Throw, Angry Baboons need to perform a different attack in order to use Throw again.
- If the party was blindsided:
- 30% chance to use Swing.
- 70% chance to attack.
- If there's one or more Big Rollers in the battle:
- If a different attack has been used since the last use of the Big Roller version of Throw:
- 70% chance to use the Big Roller verison of Throw.
- If the above did not occur, 50% chance to use Swing.
- If neither of the above ocurred, attack.
- If the Angry Baboon's HP is below 50%:
- 80% chance to use Swing.
- 20% chance to attack.
- If none of the above occurred:
- 50% chance to use Swing.
- 50% chance to attack.
- If there's one or more Rollers in the battle:
- If a different attack has been used since the last use of the Roller version of Throw:
- 70% chance to use the Roller verison of Throw.
- If the above did not occur, 50% chance to use Swing.
- If neither of the above occurred, attack.
- If the Angry Baboon's HP is below 50%:
- 80% chance to use Swing.
- 20% chance to attack.
- If none of the above occurred:
- 50% chance to use Swing.
- 50% chance to attack.
- If none of the above occurred:
- If the Angry Baboon's HP is below 50%:
- 80% chance to use Swing.
- 20% chance to attack.
- If the above didn't happen:
- 50% chance to use Swing.
- 50% chance to attack.
Drops:
 Baboon Bone: 90% chance. Sells for 10 en.
Baboon Bone: 90% chance. Sells for 10 en. Beast Bow (23 ATK, 1 Slot): Made from
Beast Bow (23 ATK, 1 Slot): Made from 1 Baboon Bone and1 Rat Hide (Tree Rat Drop 2). Costs 170 en. Bone Staff (20 ATK, 1 Slot, +1 TEC): Made from
Bone Staff (20 ATK, 1 Slot, +1 TEC): Made from 1 Baboon Bone . Costs 160 en.
 The specimens Wynne most often asks me to primarily field test on are the baboons that run about the Lush Woodlands. They are... well. Their muscle strength is quite incredible, perhaps unsurprisingly—I've been hit in the stomach a number of times by powerful swings and found myself reeling, especially in the midst of cooling down my blade. It hurts, but not nearly so much as the motherly sympathy I must find myself receiving from Dalla afterwards—I had thought I'd grown past that. I am not very fond of baboons.
The specimens Wynne most often asks me to primarily field test on are the baboons that run about the Lush Woodlands. They are... well. Their muscle strength is quite incredible, perhaps unsurprisingly—I've been hit in the stomach a number of times by powerful swings and found myself reeling, especially in the midst of cooling down my blade. It hurts, but not nearly so much as the motherly sympathy I must find myself receiving from Dalla afterwards—I had thought I'd grown past that. I am not very fond of baboons. Angry baboons are a pretty nasty wakeup call about random encounters. Up until now, you've probably been able to pretty effortlessly go through random encounters, maybe with a little bit of target prioritization if there's a tree rat in the battle, but nothing major. Yeah, no, these things have 50% more STR than a tree rat, their attack skill will seriously hurt even a fortress, and they've got triple the HP of a tree rat.
Angry baboons are a pretty nasty wakeup call about random encounters. Up until now, you've probably been able to pretty effortlessly go through random encounters, maybe with a little bit of target prioritization if there's a tree rat in the battle, but nothing major. Yeah, no, these things have 50% more STR than a tree rat, their attack skill will seriously hurt even a fortress, and they've got triple the HP of a tree rat.How do you deal with them, then? Well, look at their disable vulnerabilities. The game won't explicitly tell you this, but parties that have the ability to inflict disables would probably be inclined to try using them on angry baboons, where they wouldn't on any of the enemies they've encountered up to this point. And hey, wouldn't you know it, disables seem to stick to this thing pretty reliably, and they make the large death-causing monkey significantly easier to deal with.
It's a minor and probably obvious bit of game design, but I still appreciate it. Unfortunately, I'm in not the best shape for fighting this thing right now, in no small part because Ace is already hurt, Harper doesn't know Arm Snipe yet, and Xiaohu can only cast one spell before running out of TP.


 Nice shot, that thing's legs are real screwed up now.
Nice shot, that thing's legs are real screwed up now. Thank you.
Thank you.

 Oh man. That's not good. Seeeeeeeeein' stars.
Oh man. That's not good. Seeeeeeeeein' stars. Like I said, angry baboons hurt.
Like I said, angry baboons hurt.

 ...Tch, Eine, that's not sufficient!
...Tch, Eine, that's not sufficient! Nah, don't be so— Wuhhhohh... Hard on yourself, I can't see the stars any more! Now I'm just real dizzy...
Nah, don't be so— Wuhhhohh... Hard on yourself, I can't see the stars any more! Now I'm just real dizzy...

 Oh dear. I was hoping that would send it into convulsions...
Oh dear. I was hoping that would send it into convulsions...
 Binding the angry baboon's legs at least means I have a guarantee it'll act after everyone else, so Eine can get some major healing to Ace before the next attack occurs.
Binding the angry baboon's legs at least means I have a guarantee it'll act after everyone else, so Eine can get some major healing to Ace before the next attack occurs.
 Not even...gonna try to fight this one, sorry.
Not even...gonna try to fight this one, sorry.
 Okay, phew, that's much better.
Okay, phew, that's much better. Part of being a good field medic is knowing when your own treatments are not going to be enough.
Part of being a good field medic is knowing when your own treatments are not going to be enough. This is why I bought those medicas earlier, it's situations like this. At these very early levels, medics' healing just does not compare well to that of medicas.
This is why I bought those medicas earlier, it's situations like this. At these very early levels, medics' healing just does not compare well to that of medicas.
 ...I don't think I'm hurting it much.
...I don't think I'm hurting it much.

 Okay! That's better. Doesn't feel like I got...all of my blood punched out. We're fine.
Okay! That's better. Doesn't feel like I got...all of my blood punched out. We're fine.

 Would that I had not exhausted myself...
Would that I had not exhausted myself...

 I'm at my limit... Can't even stand...
I'm at my limit... Can't even stand... Shelly!
Shelly! Well, that just made things far harder. Shelly was the one dealing the most damage to the baboon.
Well, that just made things far harder. Shelly was the one dealing the most damage to the baboon.

 Frickin' stars, get out of my eyes!
Frickin' stars, get out of my eyes!
 I start having Xiaohu uses medicas on Ace too, leaving Harper as the only party member dealing damage.
I start having Xiaohu uses medicas on Ace too, leaving Harper as the only party member dealing damage.
 Nnnn...
Nnnn... Harper, unfortunately, is not dealing much damage to the baboon.
Harper, unfortunately, is not dealing much damage to the baboon.

 Heh...heh heh... Can't keep this up much longer, I bet!
Heh...heh heh... Can't keep this up much longer, I bet!

 Whoops, dead wroooong...
Whoops, dead wroooong... ...This is suboptimal.
...This is suboptimal.
 Especially now that the baboon can rush us directly...
Especially now that the baboon can rush us directly... The old Etrian Odyssey salt-in-the-wound: when your front row dies, your party's rows swap, putting your frail backliners in the front all of a sudden.
The old Etrian Odyssey salt-in-the-wound: when your front row dies, your party's rows swap, putting your frail backliners in the front all of a sudden.
 Just whack it...hard as you can...
Just whack it...hard as you can... All I can do is auto-battle and pray I make it out of this alive.
All I can do is auto-battle and pray I make it out of this alive.

 Ngrk...!
Ngrk...! Yeah, Eine didn't really stand a chance there...
Yeah, Eine didn't really stand a chance there...

 ...Phew.
...Phew.

 I believe, Lady Harper...that you've saved us from an early demise.
I believe, Lady Harper...that you've saved us from an early demise. ...We should perhaps return to town and seek medical attention for these three.
...We should perhaps return to town and seek medical attention for these three. Mhm.
Mhm. That fight went almost as poorly as possible. Only way it could've been worse was if I got a game over. But, well, any battle you can walk away from is a good one, and all that.
That fight went almost as poorly as possible. Only way it could've been worse was if I got a game over. But, well, any battle you can walk away from is a good one, and all that.
 Off we go.
Off we go.

 Holy hells, a walking lion!
Holy hells, a walking lion! ...That is getting a bit tiresome. Two Ariadne threads, please.
...That is getting a bit tiresome. Two Ariadne threads, please. Holy hells, a walking talking lion!
Holy hells, a walking talking lion! Yes, my name is Naijou, I'm a member of the Daffodil Guild.
Yes, my name is Naijou, I'm a member of the Daffodil Guild. Where's the blonde girl what always does the shoppin' for ya guys?
Where's the blonde girl what always does the shoppin' for ya guys? The exploration group encountered some mortal peril today, and three of them needed medical attention. Thus, in lieu of Harper, I am handling duties of commerce.
The exploration group encountered some mortal peril today, and three of them needed medical attention. Thus, in lieu of Harper, I am handling duties of commerce. Yikes. Hope everyone's okay.
Yikes. Hope everyone's okay.
 They'll be fine, they were able to make it out. Now, I have several boxes' worth of materials to sell to you...
They'll be fine, they were able to make it out. Now, I have several boxes' worth of materials to sell to you... Cheesum craps, that's a lotta mats. Lessee...
Cheesum craps, that's a lotta mats. Lessee...Berund Atelier has the following new items in stock:
 Kopis (27 ATK, 2 Slots): Made from
Kopis (27 ATK, 2 Slots): Made from 2 Rat Fangs (Tree Rat Drop 1). Costs 180 en. Makiri (22 ATK, 3 Slots): Made from
Makiri (22 ATK, 3 Slots): Made from 1 Grasseater Jaw (Grasseater Drop 2). Costs 150 en. Bone Staff (20 ATK, 1 Slot, +1 TEC): Made from
Bone Staff (20 ATK, 1 Slot, +1 TEC): Made from 1 Baboon Bone (Angry Baboon Drop). Costs 160 en. Scale Mail (26 DEF): Made from
Scale Mail (26 DEF): Made from 1 Roller Shell (Roller Drop 2) and1 Thin Wing (Woodfly Drop 2). Costs 390 en. Scale Jerkin (17 DEF): Made from
Scale Jerkin (17 DEF): Made from 1 Hard Skin (Roller Drop 1). Costs 150 en. Nectar: Made from
Nectar: Made from 1 Small Flower (Take: Multiple Sources). Costs 200 en. Theriaca B: Made from
Theriaca B: Made from 1 Forest Aloe (Take: Multiple Sources). Costs 90 en. Blind Gas: Made from
Blind Gas: Made from 2 Gritty Scales (Woodfly Drop 1). Costs 150 en.
 Hey, look, we've got new consumables we can buy from Wynne.
Hey, look, we've got new consumables we can buy from Wynne.Sadly, nectars have eaten a pretty steep price increase since EO3, where they only cost 50 en. Like every other item in EO4, they also consume materials on purchase, and must be restocked after a certain point. There's thankfully a better way of farming small flowers not too far into the game, but it's still a pain to have to go back and restock them.
I will note, before we move on, that curative consumables—medicas, nectars, theriacas, and the others—have ±0 speed modifiers.
A 40% base chance might seem fairly low, but remember, this targets every enemy. Sand Throw caps out at a 70% base chance, but is single-target. It can be multi-target with Spread Throw, but that's all the way in Veteran, and requires either two turns to set up, or an Auto-Spread activation (which, itself, is further gated behind Master). For a more fair comparison, arcanist circles' initial infliction attempts also target all enemies, and generally cap out at a 45% base chance. The gasses are not bad, by any means! Unfortunately, there are no tangler items in EO4—same idea as gasses, but for binds, instead. Those were introduced in EOU.
 I remember using blind gases on the final boss of EO5.
I remember using blind gases on the final boss of EO5. I used sleep gasses, if I remember right, since Clarste advocated for using sleep against Jaryuu, but I still didn't think much of the items. My way of looking at the effectiveness of skills and strategies in this series has evolved a lot over the past few years!
I used sleep gasses, if I remember right, since Clarste advocated for using sleep against Jaryuu, but I still didn't think much of the items. My way of looking at the effectiveness of skills and strategies in this series has evolved a lot over the past few years! Oh, 'fore I forget, since we can make kopides again, ya done with that request. Thanks bunches! Ya can grab the reward at the bar whenever ya feel like it. Or, uh, whenever ya friends are feelin' better.
Oh, 'fore I forget, since we can make kopides again, ya done with that request. Thanks bunches! Ya can grab the reward at the bar whenever ya feel like it. Or, uh, whenever ya friends are feelin' better. Hopefully that won't be too long.
Hopefully that won't be too long. I don't really have anywhere I can fit this in the narrative, so here's Wynne's normal talk dialogue right now.
I don't really have anywhere I can fit this in the narrative, so here's Wynne's normal talk dialogue right now. I heard yas started poking around da Lush Woodlands. Ya do gots yourself an Ariadne Thread, right? Don't come crying ta me if ya forget ta buy one when you're smack dab inna labyrint already. I guess ya could buy a bunch so ya always gots one, but then ya might not notice if ya run out... Huh! I guess it's best to check your stuff every time ya leave. Some explorers even write it on da map!
I heard yas started poking around da Lush Woodlands. Ya do gots yourself an Ariadne Thread, right? Don't come crying ta me if ya forget ta buy one when you're smack dab inna labyrint already. I guess ya could buy a bunch so ya always gots one, but then ya might not notice if ya run out... Huh! I guess it's best to check your stuff every time ya leave. Some explorers even write it on da map! I can't say I've ever used the note feature for anything besides, like, marking star/moon doors in EO3.
I can't say I've ever used the note feature for anything besides, like, marking star/moon doors in EO3. I occasionally find myself needing to use it for if there are teleport mazes and I need to mark down there things go.
I occasionally find myself needing to use it for if there are teleport mazes and I need to mark down there things go. I have retroactively made myself a liar, I'm doing a new playthrough of EO2U after five years since the last time I really seriously played the game, and I'm using the notes feature to mark what ingredients come from what food points.
I have retroactively made myself a liar, I'm doing a new playthrough of EO2U after five years since the last time I really seriously played the game, and I'm using the notes feature to mark what ingredients come from what food points.

 Good day, might I speak with the proprietor? My name is Naijou, I'm with the Daffodil Guild, and we would like to report completion of a quest.
Good day, might I speak with the proprietor? My name is Naijou, I'm with the Daffodil Guild, and we would like to report completion of a quest. Good day to you as well, sir.
Good day to you as well, sir. Y-You're not disturbed by my appearance?
Y-You're not disturbed by my appearance? Not particularly. You walk the same as any other patron.
Not particularly. You walk the same as any other patron. Oh, thank mercy.
Oh, thank mercy. ...Ahem. Back to business. Did Miss Wynne from the atelier let you know that we finished the quest regarding the rat fangs?
...Ahem. Back to business. Did Miss Wynne from the atelier let you know that we finished the quest regarding the rat fangs? Indeed. The reward is...two ariadne threads.
Indeed. The reward is...two ariadne threads. Well, I suppose more of these couldn't hurt...
Well, I suppose more of these couldn't hurt...


 Now I have four threads in my pack. Super.
Now I have four threads in my pack. Super.

 Two bar patrons got added to the list when I wasn't looking. I assume they're added after you first enter Lush Woodlands B1F.
Two bar patrons got added to the list when I wasn't looking. I assume they're added after you first enter Lush Woodlands B1F.Apple-cheeked explorer:
 Ooh, ooh, are you part of the Daffodil Guild?
Ooh, ooh, are you part of the Daffodil Guild? Yes.
Yes. Wowwwww, not only are they moving so fast, they've got a walking lion! Mind if I give you some advice?
Wowwwww, not only are they moving so fast, they've got a walking lion! Mind if I give you some advice? I am not a lion. But yes, go ahead.
I am not a lion. But yes, go ahead. Okay, okay, both of these are for when you're out flying. First...the dragon! If you see it in the sky, don't do anything crazy. Just coming near that enormous, bright red fire dragon will provoke it into tearing you to tiny pieces! Second...the pooka! It's so cute that no amount of skill will result in anything but disaster! It's said that whoever catches one is guaranteed good luck... But even if you find one, it fluffily runs away! Do they hate me that much!?
Okay, okay, both of these are for when you're out flying. First...the dragon! If you see it in the sky, don't do anything crazy. Just coming near that enormous, bright red fire dragon will provoke it into tearing you to tiny pieces! Second...the pooka! It's so cute that no amount of skill will result in anything but disaster! It's said that whoever catches one is guaranteed good luck... But even if you find one, it fluffily runs away! Do they hate me that much!? We've already seen pookas, but what's all this about a dragon...? That's ominous.
We've already seen pookas, but what's all this about a dragon...? That's ominous.Haunted runemaster Menou:
 Excuse me, ma'am?
Excuse me, ma'am? Yes? I'm busy studying the Monstrous Codex... Your guild does pay attention to the Codex, I hope. It lists the weaknesses of monsters and the materials they drop. It's like a manual for explorers.
Yes? I'm busy studying the Monstrous Codex... Your guild does pay attention to the Codex, I hope. It lists the weaknesses of monsters and the materials they drop. It's like a manual for explorers. ...I was going to ask if you had any information for us, but that will do nicely. Thank you.
...I was going to ask if you had any information for us, but that will do nicely. Thank you. Mhm. Now go away. I'm busy...
Mhm. Now go away. I'm busy... The Codex, sadly, does not list disable resistances, and will not do that until EO2U. Honestly, it's mostly useful for tracking what monster drops you haven't gotten yet.
The Codex, sadly, does not list disable resistances, and will not do that until EO2U. Honestly, it's mostly useful for tracking what monster drops you haven't gotten yet.


 After the utter disaster that was the run-in with an angry baboon, I spend over half my money on an armor upgrade for Ace. Armor may suck in EO4, but that doesn't mean it can be entirely ignored.
After the utter disaster that was the run-in with an angry baboon, I spend over half my money on an armor upgrade for Ace. Armor may suck in EO4, but that doesn't mean it can be entirely ignored.
 Ah, stupendous, you all are fine.
Ah, stupendous, you all are fine. A little sore, but yep.
A little sore, but yep. Many thanks, Lady— Ah, my apologies, but what is your name?
Many thanks, Lady— Ah, my apologies, but what is your name? Dalla. Be safe on your next time out, dearies.
Dalla. Be safe on your next time out, dearies.
 Can we visit the cargo wharf before we go again?
Can we visit the cargo wharf before we go again? Any particular reason why?
Any particular reason why? We haven't been there yet.
We haven't been there yet. ...Yeah, fair.
...Yeah, fair.
 The wharf is where Tharsis opens up to the outside world... Many a merchant comes here to trade. Explorers come and go as they please, too, seeing as this is where we fix up their skyships.
The wharf is where Tharsis opens up to the outside world... Many a merchant comes here to trade. Explorers come and go as they please, too, seeing as this is where we fix up their skyships. So many people...
So many people... Yep. If yeh're a fan of people-watching, yeh can't beat spending an afternoon here. Oh, let me give yeh this before I forget.
Yep. If yeh're a fan of people-watching, yeh can't beat spending an afternoon here. Oh, let me give yeh this before I forget.
 That's for your skyship. It should help yeh find some of that treasure sleeping in the great wide world.
That's for your skyship. It should help yeh find some of that treasure sleeping in the great wide world. You have my attention! Where— Do you know where we can use this thing?
You have my attention! Where— Do you know where we can use this thing? If I knew that, then I'd've dug up the treasure myself already! Yeh're gonna have to ask other explorers about that.
If I knew that, then I'd've dug up the treasure myself already! Yeh're gonna have to ask other explorers about that.
 The cargo wharf is where we go to handle anything QR code and StreetPass-related, acting as a partial replacement for Inver Port from EO3. The 3DS made a big push for a sort of passive form of multiplayer, and the EO series happily jumped on. Well, to be truthful, EO already had jumped on it, back on the DS! EO3 let you put your DS into sleep-mode-with-wireless-communications-enabled in order to exchange guild cards. EO4 took that idea and made it work through StreetPass instead, and it worked pretty well, back when people used to carry around 3DSes. Even in the United States, noted not-very-dense country with nowhere near as many people carrying around 3DSes as compared to Japan, I still accumulated a lot of EO4, EOU, and EO2U guild cards through StreetPass, just walking around airports—or even just around my college campus sometimes!
The cargo wharf is where we go to handle anything QR code and StreetPass-related, acting as a partial replacement for Inver Port from EO3. The 3DS made a big push for a sort of passive form of multiplayer, and the EO series happily jumped on. Well, to be truthful, EO already had jumped on it, back on the DS! EO3 let you put your DS into sleep-mode-with-wireless-communications-enabled in order to exchange guild cards. EO4 took that idea and made it work through StreetPass instead, and it worked pretty well, back when people used to carry around 3DSes. Even in the United States, noted not-very-dense country with nowhere near as many people carrying around 3DSes as compared to Japan, I still accumulated a lot of EO4, EOU, and EO2U guild cards through StreetPass, just walking around airports—or even just around my college campus sometimes!Oh, right, uh, what can we actually use guild cards or QR codes for? Well, EO4 attempted to do new things with these new features, so you can use other peoples' guild cards not only to get locations of dowsing rod treasures, but also to recruit guest party members, a feature that has a lot of very strange balance considerations. I'll try to show it off at some point, but I won't be making active use of it.
There's another function for QR codes specifically: promotional quests distributed through QR codes! I'll go over those later, but in short they're a strange form of free DLC? There's even content related to them that was translated but never distributed for the North American and European versions of the game. I considered finding a way to show them off, mostly by mucking about with the internal data, but after looking at the quests, there just...really isn't much there. Oh well. There are some interesting things to be talked about regarding the ones that were distributed, though.


 You can also...check your Yggdrasil code! What's that? What was it used for? Was it even used for anything? Was it used for something in Japan but not North America or Europe?
You can also...check your Yggdrasil code! What's that? What was it used for? Was it even used for anything? Was it used for something in Japan but not North America or Europe?I'unno.
 If you aren't able to recite your Yggdrasil Code after you die, you'll be drafted into the skeleton war by the Undead King.
If you aren't able to recite your Yggdrasil Code after you die, you'll be drafted into the skeleton war by the Undead King. Is that what happened to the landsknecht and sniper that the Undead King summons?
Is that what happened to the landsknecht and sniper that the Undead King summons?
 You can also write extra data to your 3DS. When you do this, it basically just writes information about your party to a file on your 3DS. What use does that have?
You can also write extra data to your 3DS. When you do this, it basically just writes information about your party to a file on your 3DS. What use does that have?None. No other games read EO4's extra data.
I imagine future EO games were meant to use this data for some kind of interconnectivity, similar to how you could use game clear passwords from EO1 in EO2, but that never materialized. EOU has the same option to write data about your party to extra data, and that is actually used in EO2U. If you write EOU extdata and then play EO2U, you can encounter extra grimoire trade NPCs at the restaurant, who carry grimoire stones similar to the ones your EOU party were carrying. They also, if I remember correctly, are named "legendary landsknecht" or "legendary gunner" based on the character's class.
Anyway, before we leave the cargo wharf, I'll note that no facility like it showed up in future games. The guild bases in the Untolds—the mansion in EOU, and the restaurant in EO2U—inherited the QR scanning and guild card management functions after the cargo wharf's demise. EO5 then moved those functions to the inn, and they remained there in EON, owing to EO5 removing the guild bases.



 Food. Sorry, it doesn't have sauce.
Food. Sorry, it doesn't have sauce. Oh man that smells good.
Oh man that smells good. Yep, tastes good, too.
Yep, tastes good, too. I actually remembered to eat food before going into the labyrinth this time. +1 STR, woo.
I actually remembered to eat food before going into the labyrinth this time. +1 STR, woo.


 A simple rush will do for clearing this passageway.
A simple rush will do for clearing this passageway. Not gonna hear me complaining! Here I go!
Not gonna hear me complaining! Here I go!

 I managed to fight an angry baboon without anyone dying! My reward is level ups for Harper and Xiaohu.
I managed to fight an angry baboon without anyone dying! My reward is level ups for Harper and Xiaohu.

 There. Angry baboons should give me significantly less trouble now. Beyond the fact that binding their arms disables Swing, arm binds also halve the target's STR, so that'll significantly reduce the damage that angry baboons can deal with normal attacks.
There. Angry baboons should give me significantly less trouble now. Beyond the fact that binding their arms disables Swing, arm binds also halve the target's STR, so that'll significantly reduce the damage that angry baboons can deal with normal attacks.

 Xiaohu gets another rank of Runic Gleam.
Xiaohu gets another rank of Runic Gleam.

 Nice find.
Nice find. Thank you. This one seemed a bit sturdier than the others, making gathering it much simpler.
Thank you. This one seemed a bit sturdier than the others, making gathering it much simpler. You'll get a message like this when a character's gathering skill activates.
You'll get a message like this when a character's gathering skill activates.

 Another baboon's demise gives the other three members of the party a level.
Another baboon's demise gives the other three members of the party a level.

 I decide to have Shelly get more ranks of Vanguard, in preparation for fights against FOEs and bosses.
I decide to have Shelly get more ranks of Vanguard, in preparation for fights against FOEs and bosses.

 Ace maxes out Auto-Taunt, giving her a whopping 50% chance to automatically activate it for free at the start of every battle. Nice!
Ace maxes out Auto-Taunt, giving her a whopping 50% chance to automatically activate it for free at the start of every battle. Nice!

 Eine raises Healing to rank 3, and unlocks Line Heal as a result. Line Heal is a row-target HP-restoring skill, if the name didn't give it away. It restores less HP than Healing, but, well, it's row-target.
Eine raises Healing to rank 3, and unlocks Line Heal as a result. Line Heal is a row-target HP-restoring skill, if the name didn't give it away. It restores less HP than Healing, but, well, it's row-target.Should note that, unlike most other EO games, all of the medic's raw HP-restoring skills have the same speed modifiers, so they're all equally slow.


 Great. Another bear.
Great. Another bear. They seem to lack peripheral vision. I'm surprised it hasn't noticed us yet.
They seem to lack peripheral vision. I'm surprised it hasn't noticed us yet.

 Ah, there it goes...
Ah, there it goes... I haven't explicitly mentioned it yet, so: FOE icons on the map turn red when an FOE is actively pursuing you.
I haven't explicitly mentioned it yet, so: FOE icons on the map turn red when an FOE is actively pursuing you.

 I wonder why it didn't destroy those trees before.
I wonder why it didn't destroy those trees before. Is it even partaking of the sap?
Is it even partaking of the sap? Doesn't look like it to me.
Doesn't look like it to me. What a strange creature.
What a strange creature.

 Looks like it's got a short attention span, too. Soon as we get just a bit away from it, it's back to looking at the trees.
Looks like it's got a short attention span, too. Soon as we get just a bit away from it, it's back to looking at the trees.

 Now is a good time to mention that EO4 was the first EO game to introduce the concept of enemies being able to have both a front and back row, like the party. Already, the game is taking advantage of that, by placing the fragile woodfly in the back row, and (theoretically) sturdy rollers in the front. Until the woodfly can be killed, it'll be inflicting blind on various party members, making it harder to break through the wall of rollers, you get the idea.
Now is a good time to mention that EO4 was the first EO game to introduce the concept of enemies being able to have both a front and back row, like the party. Already, the game is taking advantage of that, by placing the fragile woodfly in the back row, and (theoretically) sturdy rollers in the front. Until the woodfly can be killed, it'll be inflicting blind on various party members, making it harder to break through the wall of rollers, you get the idea.This is a very tame example of the kind of awful trickery the game can pull with enemy rows. We'll begin to see some crueler stuff as the game goes on, and future EO games can get real nasty with back-row dilemmas.


 Hell yeah, we got through the first floor! And all without any big cats wiping out our group!
Hell yeah, we got through the first floor! And all without any big cats wiping out our group! Is that...a common occurrence, back in Armoroad?
Is that...a common occurrence, back in Armoroad? Yes. Every week, you'd get at least one group of five dragged out of the first floor, either badly wounded or just straight-up dead. Rest of their guild usually either found more peaceful work in town, or went back home on the next ship out of town.
Yes. Every week, you'd get at least one group of five dragged out of the first floor, either badly wounded or just straight-up dead. Rest of their guild usually either found more peaceful work in town, or went back home on the next ship out of town. You say that, but the baboon—
You say that, but the baboon— That thing isn't shit compared to the cats. Harper can break those things' arms with just a bow and arrow. Y'know how we'd do that in Armoroad? You'd have to summon a fuckin' snake to do it for you! Took forever, and always exhausted the hell out of whoever was doing it. Hell, even then, all that'd do is make it have less good of a grip on whoever it bit.
That thing isn't shit compared to the cats. Harper can break those things' arms with just a bow and arrow. Y'know how we'd do that in Armoroad? You'd have to summon a fuckin' snake to do it for you! Took forever, and always exhausted the hell out of whoever was doing it. Hell, even then, all that'd do is make it have less good of a grip on whoever it bit. Us having prior experience from the Old Forest Mine likely helped our survival, no?
Us having prior experience from the Old Forest Mine likely helped our survival, no? Man, yeah, that's a good—
Man, yeah, that's a good— Clear the way, injured guards coming through!
Clear the way, injured guards coming through! That sounds bad.
That sounds bad.
 Hi, Whirlwind. What's wrong? Your face is scrunched.
Hi, Whirlwind. What's wrong? Your face is scrunched. Well, besides the guards being carried out...
Well, besides the guards being carried out... That man you're carrying...is not moving.
That man you're carrying...is not moving. Yep. Don't have much time to chat. This poor Tharsis boy... Whatever's down there, it's bad news.
Yep. Don't have much time to chat. This poor Tharsis boy... Whatever's down there, it's bad news. Though the man projects a calm demeanor, his fatigue shows through in the sweat pouring down his brow. You suspect he may require help...
Though the man projects a calm demeanor, his fatigue shows through in the sweat pouring down his brow. You suspect he may require help... Can I be of assistance? I may not be able to resuscitate him, but I at least can bandage wounds...
Can I be of assistance? I may not be able to resuscitate him, but I at least can bandage wounds... Mighty kind of you, but he's going to need some serious help. Whatever's down there, once those guards and this guy get back to town, I bet you the Count's gonna want something done about this.
Mighty kind of you, but he's going to need some serious help. Whatever's down there, once those guards and this guy get back to town, I bet you the Count's gonna want something done about this. Mm. Well, we'd best not keep you any longer.
Mm. Well, we'd best not keep you any longer. Appreciate it. Be careful if you're heading down there. This guy was by no means a greenhorn explorer.
Appreciate it. Be careful if you're heading down there. This guy was by no means a greenhorn explorer.
 ...Let's at least see what's down the stairs first, then we'll head back to town.
...Let's at least see what's down the stairs first, then we'll head back to town.

 No immediate threats. Alright, we're leaving.
No immediate threats. Alright, we're leaving.

 There is anger in their voices as they say things such as...
There is anger in their voices as they say things such as... That monster...!
That monster...! We can't let this stand!
We can't let this stand! No points for guessing what they're mad about.
No points for guessing what they're mad about.
 Were you able to get that man to the hospital?
Were you able to get that man to the hospital? Yeah, don't worry. His wounds were bad, but not grievous. He'll be in the hospital for a while, but he'll live. Sounds like most of the guards weren't so lucky, though.
Yeah, don't worry. His wounds were bad, but not grievous. He'll be in the hospital for a while, but he'll live. Sounds like most of the guards weren't so lucky, though. Is there some particularly vicious monster on the second floor?
Is there some particularly vicious monster on the second floor? Bingo. A huge bear with blood-red fur. The Outland Count's probably already got a mission for that monster's head, but if you want my advice? Don't go down there yet. Even beyond the red bear, the monsters down there are no joke.
Bingo. A huge bear with blood-red fur. The Outland Count's probably already got a mission for that monster's head, but if you want my advice? Don't go down there yet. Even beyond the red bear, the monsters down there are no joke. Would one of those smaller mazes help us get stronger?
Would one of those smaller mazes help us get stronger? I was actually just about to suggest you go there, yeah. The Small Orchard's not far from the Lush Woodlands—you'll have an easier time of things there. Ack, look at the time, I need to get going. Don't do anything reckless, Daffodil Guild. That'll lead nowhere but trouble...
I was actually just about to suggest you go there, yeah. The Small Orchard's not far from the Lush Woodlands—you'll have an easier time of things there. Ack, look at the time, I need to get going. Don't do anything reckless, Daffodil Guild. That'll lead nowhere but trouble... Whirlwind chuckles as he walks towards the city gates.
Whirlwind chuckles as he walks towards the city gates. ...Let's get going.
...Let's get going. Wait, Harper— Oh, not again...
Wait, Harper— Oh, not again...

 Mhm.
Mhm. It has claimed the lives of many of our soldiers. Left unchecked, it may prove a menace to you explorers, too.
It has claimed the lives of many of our soldiers. Left unchecked, it may prove a menace to you explorers, too. ...Mhm.
...Mhm. Harper, please, stop running ahead of the rest of us...
Harper, please, stop running ahead of the rest of us... I can't run so good, heh...
I can't run so good, heh... Ah, I was wondering where the rest of your group was. Now that you're all here, I feel that I should inform you that I've issued a mission to subjugate the beast that caused all of this. This task is dangerous, no doubt, but it must be done.
Ah, I was wondering where the rest of your group was. Now that you're all here, I feel that I should inform you that I've issued a mission to subjugate the beast that caused all of this. This task is dangerous, no doubt, but it must be done.
 We will need to take some time to train, but...we will accept, nonetheless.
We will need to take some time to train, but...we will accept, nonetheless. Splendid, your guild has proven itself reliable so far. If that beast is allowed to run amok on the lower floors, who knows how many more lives it may claim, between the guards and less-experienced explorers. Your mission is to eliminate the monster—which some of the guards have taken to calling "the Bloodbear."
Splendid, your guild has proven itself reliable so far. If that beast is allowed to run amok on the lower floors, who knows how many more lives it may claim, between the guards and less-experienced explorers. Your mission is to eliminate the monster—which some of the guards have taken to calling "the Bloodbear." Yeah, we...kinda got that.
Yeah, we...kinda got that. Ah, I'm repeating myself. Bad habit, you know. Moving on, since this mission is exceptionally dangerous, I've instructed the guildmaster to instruct you in the use of special techniques that will undoubtedly prove vital in your continued success.
Ah, I'm repeating myself. Bad habit, you know. Moving on, since this mission is exceptionally dangerous, I've instructed the guildmaster to instruct you in the use of special techniques that will undoubtedly prove vital in your continued success. Oh, shit, special techniques from Teach? Count me interested.
Oh, shit, special techniques from Teach? Count me interested. That should be everything, then. Before you all go, though...
That should be everything, then. Before you all go, though...
 He seems kinda silly.
He seems kinda silly. That he does, yes. But don't let appearances fool you, he is one of Tharsis's best explorers. Played an integral role in the development of the skyships we distribute to sanctioned guilds, too! Our fair city owes much of its prosperity to him.
That he does, yes. But don't let appearances fool you, he is one of Tharsis's best explorers. Played an integral role in the development of the skyships we distribute to sanctioned guilds, too! Our fair city owes much of its prosperity to him. Huh. I'd figured he was something special going by the fact that he was just hanging out in the Old Forest Mine on his own, but still.
Huh. I'd figured he was something special going by the fact that he was just hanging out in the Old Forest Mine on his own, but still. I believe we should be going. Our guildmates will need to hear about the mission we've accepted.
I believe we should be going. Our guildmates will need to hear about the mission we've accepted. That would be for the best, yes. Safe travels.
That would be for the best, yes. Safe travels.

 Oy, it's just one thing after another...
Oy, it's just one thing after another...
 He's all fired up bout dis mission.
He's all fired up bout dis mission. I can't say I'm surprised, given the number of guards the Bloodbear killed.
I can't say I'm surprised, given the number of guards the Bloodbear killed. Ye, dark stuff. On da bright side, dat shipment of pole stones and silver whistles the Count paid for forever ago finally got in.
Ye, dark stuff. On da bright side, dat shipment of pole stones and silver whistles the Count paid for forever ago finally got in. Oh?
Oh? Eh, you're buyin' a buncha threads, you prob'ly don't have much use for these things. Pole stones take ya back to the last stairs ya used, and silver whistles'll take ya outta da labyrinth you're in, but won't take ya back ta Tharsis.
Eh, you're buyin' a buncha threads, you prob'ly don't have much use for these things. Pole stones take ya back to the last stairs ya used, and silver whistles'll take ya outta da labyrinth you're in, but won't take ya back ta Tharsis. Yeah, nah.
Yeah, nah. Figured. Still, dey're cheaper than threads, so a lotta da really cheap guilds buy a bunch, hence why da Count had ta help us restock. Oh, but here's somethin' that might catch ya attention: we fixed up da forge! Ya can modify dose weapons you've got, if'n ya want.
Figured. Still, dey're cheaper than threads, so a lotta da really cheap guilds buy a bunch, hence why da Count had ta help us restock. Oh, but here's somethin' that might catch ya attention: we fixed up da forge! Ya can modify dose weapons you've got, if'n ya want. Oh, nice. What's it cost?
Oh, nice. What's it cost? Eh? Cost? What're ya talkin' about? Just gotta make sure ya got da right mats. Ya don't gotta pay us.
Eh? Cost? What're ya talkin' about? Just gotta make sure ya got da right mats. Ya don't gotta pay us. ...Napier, you... You... Ugh.
...Napier, you... You... Ugh.
 Wow, dat interested in tryin' the forge, huh?
Wow, dat interested in tryin' the forge, huh? Nah, we've got junk to offload, first.
Nah, we've got junk to offload, first. Fine by me. Here's da junk dat junk makes.
Fine by me. Here's da junk dat junk makes.Berund Atelier has the following new items in stock:
 Beast Bow (23 ATK, 1 Slot): Made from
Beast Bow (23 ATK, 1 Slot): Made from 1 Baboon Bone (Angry Baboon Drop) and1 Rat Hide (Tree Rat Drop 2). Costs 170 en. Hide Aspis (10 DEF): Made from
Hide Aspis (10 DEF): Made from 2 Rat Hides (Tree Rat Drop 2). Costs 230 en.


 The beast bow's not a huge upgrade for Harper, but it's a cheap one. I buy it. Since it has an open forge slot...
The beast bow's not a huge upgrade for Harper, but it's a cheap one. I buy it. Since it has an open forge slot...
 So, how's this forging thing work, for the rest of 'em? I already know.
So, how's this forging thing work, for the rest of 'em? I already know. Pick da hammer dat gives da thing ya want, put some'a the mats that make up da weapon on top'a it, and just whack away until da weapon looks good as new.
Pick da hammer dat gives da thing ya want, put some'a the mats that make up da weapon on top'a it, and just whack away until da weapon looks good as new. You don't seem to have very many hammers available, though.
You don't seem to have very many hammers available, though. These things're expensive!
These things're expensive! Forging lets you apply supplemental effects and/or buffs to weapons. It was introduced in EO3, but was sort of unbearable to deal with in that game, between the money cost, the material cost, and the severe lack of forgeable slots in that game. The fundamental system is unchanged in EO4, but a lot of the annoyances have been stripped out. While you still do have to consume materials to forge weapons, you no longer have to pay money alongside that.
Forging lets you apply supplemental effects and/or buffs to weapons. It was introduced in EO3, but was sort of unbearable to deal with in that game, between the money cost, the material cost, and the severe lack of forgeable slots in that game. The fundamental system is unchanged in EO4, but a lot of the annoyances have been stripped out. While you still do have to consume materials to forge weapons, you no longer have to pay money alongside that.Additionally, a few new forge types have been added to fill in some pretty obvious holes in EO3's selection. Probably the most important is the ELM forge, an elemental counterpart to ATK. ATK forges increase physical damage dealt with the weapon by 3% per forge instance, and ELM forges increase elemental damage dealt with the weapon by 3% per forge instance. If we're talking physical/elemental composite damage, than both ATK and ELM forges work. These are absolutely the most generically useful forges, and get ready to see me making a lot of ATK/ELM forges as the game goes on.
Aside from that, right now, we've just got VIT forges, and blind forges. Stat forges are very simple, they just give +1 of a given stat per forge. Putting two VIT forges on a weapon would give the wielder +2 VIT. Disable forges, which includes the blind forges, give normal attacks a chance to inflict the given disable, with the base chance depending on the number of forges on the weapon. For normal ailments, plus binds, the first disable forge on a weapon gives +6% base chance, while further ones give +3%.
An important note here is that, while defensive equipment uses forges to give their bonuses, some forge types work differently on them. Disable forges on defensive equipment, for example, give +10% resistance to that disable.

 That was easy. Yay.
That was easy. Yay. Harper gets a whopping +3% physical damage on her bow. That was more to show the system in action than anything, really.
Harper gets a whopping +3% physical damage on her bow. That was more to show the system in action than anything, really.


 Since we have some money to spare, I buy power rings for Shelly and Harper, and smart earrings for Xiaohu. This should help these three just generally deal more damage. +5 STR/TEC is a lot this early on.
Since we have some money to spare, I buy power rings for Shelly and Harper, and smart earrings for Xiaohu. This should help these three just generally deal more damage. +5 STR/TEC is a lot this early on.
 The hammer clued me into that, yes.
The hammer clued me into that, yes.  Have you been doing this for long, Miss Wynne?
Have you been doing this for long, Miss Wynne? Ehh, not really. I'm still just an apprennice...
Ehh, not really. I'm still just an apprennice...
 Thank you for sharing.
Thank you for sharing. ...I'm confused. What did she mean by that?
...I'm confused. What did she mean by that? It means something really personal. Or that she's really enthusiastic.
It means something really personal. Or that she's really enthusiastic. Those are two very different intentions, but judging by the first one, I will not pry any further.
Those are two very different intentions, but judging by the first one, I will not pry any further. This line seemingly lives rent-free in the head of every EO4 player I've ever met.
This line seemingly lives rent-free in the head of every EO4 player I've ever met.
 A good amount of what they sell there was brought back by explorers! The food in tonight's dinner might very well have been made with the ingredients you gathered yesterday.
A good amount of what they sell there was brought back by explorers! The food in tonight's dinner might very well have been made with the ingredients you gathered yesterday. The ingredients we didn't keep in the fridge, anyway.
The ingredients we didn't keep in the fridge, anyway. Oh, you have a room for storing ingredients in your skyship?
Oh, you have a room for storing ingredients in your skyship? Yep.
Yep. That's amazing! Oh, that must be such a convenience.
That's amazing! Oh, that must be such a convenience.

 We suffered heavy injuries at the hands of a baboon, but it's otherwise been smooth sailing.
We suffered heavy injuries at the hands of a baboon, but it's otherwise been smooth sailing. One of your companions informed me of that, yes. I am glad to see that you are still with us. Where are you planning to explore next?
One of your companions informed me of that, yes. I am glad to see that you are still with us. Where are you planning to explore next? The Small Orchard, on Mister Whirlwind's suggestion.
The Small Orchard, on Mister Whirlwind's suggestion. Ah, a wise choice. I would advise that you always check our request board for anything related to the smaller caves before you head out. Though, we presently lack anything for the Small Orchard.
Ah, a wise choice. I would advise that you always check our request board for anything related to the smaller caves before you head out. Though, we presently lack anything for the Small Orchard.
 We've got bar patrons to talk to, too.
We've got bar patrons to talk to, too.Map-focused explorer:
 You guys having any trouble with the Lush Woodlands?
You guys having any trouble with the Lush Woodlands? We are a bit...hesitant to explore the second floor any further.
We are a bit...hesitant to explore the second floor any further. Same here. I went to the Small Orchard to train, but then it's got that awful deer that's faster than me... I dunno, I feel like I should stay home. Both the second floor and the Small Orchard are a pain.
Same here. I went to the Small Orchard to train, but then it's got that awful deer that's faster than me... I dunno, I feel like I should stay home. Both the second floor and the Small Orchard are a pain. With that kinda attitude, maybe it's best that you stay home anyway.
With that kinda attitude, maybe it's best that you stay home anyway. Perky dancer:
Perky dancer: Heyyyyy, you guys having any money troubles?
Heyyyyy, you guys having any money troubles? Not really. Gathering stuff's worth a good amount.
Not really. Gathering stuff's worth a good amount. Aw, that's just what I was about to recommend. Pooh, it's no fun when people discover things on their own...
Aw, that's just what I was about to recommend. Pooh, it's no fun when people discover things on their own... Womanizing sniper:
Womanizing sniper: Heyyy, little lady, you look like a fellow sniper.
Heyyy, little lady, you look like a fellow sniper. Mhm.
Mhm. Man, us snipers sure are something else, huh? Enemies too fast to hit? Pshaw, we've got our Snipe skills. Other peeps need to hit them? That's what Spotter's for, baby.
Man, us snipers sure are something else, huh? Enemies too fast to hit? Pshaw, we've got our Snipe skills. Other peeps need to hit them? That's what Spotter's for, baby. Yup.
Yup. Bottom line? We're great.
Bottom line? We're great. Okay.
Okay. ...So, you wanna go get dinner sometime?
...So, you wanna go get dinner sometime? No. I don't like men.
No. I don't like men. Gck...! And so, womens' hearts remain the only thing I can't pierce. Everything I try is a dud...
Gck...! And so, womens' hearts remain the only thing I can't pierce. Everything I try is a dud...

 Yep. Whatcha got to teach us, Teach?
Yep. Whatcha got to teach us, Teach? You aren't going to stop calling me that, no matter how many times I ask, are you?
You aren't going to stop calling me that, no matter how many times I ask, are you? Nope.
Nope. ...Hahh. Well, if you're going to go up against the Bloodbear, you're going to need a special kind of skill.
...Hahh. Well, if you're going to go up against the Bloodbear, you're going to need a special kind of skill.


 Woah.
Woah. Those will teach you how to use burst skills. As you do battle, you'll build up a sort of communal energy. Burst skills let you tap into that energy and execute powerful techniques, on top of your normal actions. I suggest you make a habit of using them.
Those will teach you how to use burst skills. As you do battle, you'll build up a sort of communal energy. Burst skills let you tap into that energy and execute powerful techniques, on top of your normal actions. I suggest you make a habit of using them. Burst skills are EO4's replacement for limit skills. Instead of each character having an individual gauge you build up to execute special skills, burst skills in EO4 rely on the burst gauge, which is shared across all party members. I won't bore you with the exact details, but doing anything besides attempting to escape will fill the burst gauge up. Every time the burst gauge hits 100%, you get a unit of burst, which characters can then spend on burst skills. You can have a maximum of five units of burst at once, and so long as the cost doesn't exceed that, multiple characters can use burst skills within the same turn.
Burst skills are EO4's replacement for limit skills. Instead of each character having an individual gauge you build up to execute special skills, burst skills in EO4 rely on the burst gauge, which is shared across all party members. I won't bore you with the exact details, but doing anything besides attempting to escape will fill the burst gauge up. Every time the burst gauge hits 100%, you get a unit of burst, which characters can then spend on burst skills. You can have a maximum of five units of burst at once, and so long as the cost doesn't exceed that, multiple characters can use burst skills within the same turn.Out of all the "special move" systems in EO, burst is definitely the easiest to build and the easiest to use. I'm a fan of it, and I'm sort of sad it never showed up again.
Fun fact, the burst gain formula was used basically without changes for the boost gain formula in EOU, and the force gain formula in EO2U.
 Yeah, it always feels to me like they hamstrung it for Union Skills in EO5 to justify the race gimmick and then just sort of didn't bring it back afterwards because the more recent games were remakes. Explosive supermoves with Force Boost and Break are neat and all, but the Burst system is good for leveling the playing field.
Yeah, it always feels to me like they hamstrung it for Union Skills in EO5 to justify the race gimmick and then just sort of didn't bring it back afterwards because the more recent games were remakes. Explosive supermoves with Force Boost and Break are neat and all, but the Burst system is good for leveling the playing field. On another note...
On another note...
 Why don't you try to be the first? The labyrinth doesn't have feelings. It doesn't care who explores it. There's no need to tiptoe around your seniors in the guild just because you're a pack of rookies.
Why don't you try to be the first? The labyrinth doesn't have feelings. It doesn't care who explores it. There's no need to tiptoe around your seniors in the guild just because you're a pack of rookies. An excellent idea! Thank you for the information.
An excellent idea! Thank you for the information.

 Yeh weren't thinking about taking some revenge for them, right?
Yeh weren't thinking about taking some revenge for them, right? No. Our next course of action is to explore the Small Orchard.
No. Our next course of action is to explore the Small Orchard. Heh, yeh've got more sense than most explorers around these parts.
Heh, yeh've got more sense than most explorers around these parts. I believe that's the second time we've been told that, yes.
I believe that's the second time we've been told that, yes. It's because it's true. Well, careful as yeh go, Daffodil.
It's because it's true. Well, careful as yeh go, Daffodil.

 So many quests...
So many quests...Defeat a violent baboon:
 What's this one about a baboon?
What's this one about a baboon? Ah, that request... It is a task of retribution from a beginning explorer. On the first floor of the Lush Woodlands, there is a wooden box where some leave items for emergencies. Do you know it?
Ah, that request... It is a task of retribution from a beginning explorer. On the first floor of the Lush Woodlands, there is a wooden box where some leave items for emergencies. Do you know it? Mhm. We left an Ariadne thread there.
Mhm. We left an Ariadne thread there. How kind of you. Unfortunately, that box is frequently the target of angry baboon attacks. It would seem they have picked up on the fact that explorers are frequently at that location.
How kind of you. Unfortunately, that box is frequently the target of angry baboon attacks. It would seem they have picked up on the fact that explorers are frequently at that location. Well, after that first run-in with those damn monkeys, we know how to take them on, so this should be easy.
Well, after that first run-in with those damn monkeys, we know how to take them on, so this should be easy. Heartening words. If you would like further advice, though, the man wearing the...ahem, the baboon head, would be more than happy to provide.
Heartening words. If you would like further advice, though, the man wearing the...ahem, the baboon head, would be more than happy to provide. ...Nnn.
...Nnn. Culantro, please:
Culantro, please: Oh, Lady Dalla posted a request?
Oh, Lady Dalla posted a request? Ah, yes, I would appreciate it if you would handle it. She wants someone to retrieve an herb called culantro, which grows on the first floor of the Lush Woodlands. I am told that it is in a hidden area, near the northern part of the floor.
Ah, yes, I would appreciate it if you would handle it. She wants someone to retrieve an herb called culantro, which grows on the first floor of the Lush Woodlands. I am told that it is in a hidden area, near the northern part of the floor. The smelly plant room?
The smelly plant room? Ah, you already know where to look, good.
Ah, you already know where to look, good. I have that gene that makes cilantro taste like soap. What does cilantro taste like to people who do not have this gene.
I have that gene that makes cilantro taste like soap. What does cilantro taste like to people who do not have this gene. I don't believe I've ever had anything with cilantro on it, so I couldn't tell you.
I don't believe I've ever had anything with cilantro on it, so I couldn't tell you.There's text in the game for if you already have culantro in your inventory, but I'm pretty sure that's impossible to ever see, since the ability to gather culantro isn't enabled until you take this quest.
Find the headwaters:
 Another Count request, huh.
Another Count request, huh. Yes, he wishes to know where the river near our city flows from. You can learn more by talking to him.
Yes, he wishes to know where the river near our city flows from. You can learn more by talking to him. This should be easy, we've already marked where the source is.
This should be easy, we've already marked where the source is. This exclamation point.
This exclamation point. Atelier request II:
Atelier request II: Another request from Miss Wynne? So soon?
Another request from Miss Wynne? So soon? She wishes to obtain some dragon's blood—I gather that it is a type of herb. I imagine she could give you more details.
She wishes to obtain some dragon's blood—I gather that it is a type of herb. I imagine she could give you more details. Hole-y terror:
Hole-y terror: Ah, while you're here, may I interest you in this request? Your guild seems to be the only one capable of making any headway into the second floor, and coming back without injury. I say this, because, well...
Ah, while you're here, may I interest you in this request? Your guild seems to be the only one capable of making any headway into the second floor, and coming back without injury. I say this, because, well... Some gutsy bastard went deep into the second floor and lost something after he had to run. That's my guess, looking at the posting.
Some gutsy bastard went deep into the second floor and lost something after he had to run. That's my guess, looking at the posting. That is a fair assessment. The client noticed a hole in an unnaturally caved-in area on the southern path, and decided to investigate.
That is a fair assessment. The client noticed a hole in an unnaturally caved-in area on the southern path, and decided to investigate. ...At night.
...At night. Why would you do that?
Why would you do that? You'd have to ask the client, unfortunately. The way he described it to me, a horrific monster then emerged from the hole, and attacked him. He wishes to confirm if the monster is still there, and suggests returning at night, like he did.
You'd have to ask the client, unfortunately. The way he described it to me, a horrific monster then emerged from the hole, and attacked him. He wishes to confirm if the monster is still there, and suggests returning at night, like he did. Dumb bastard. Ah, I mean, yeah, we'll do it. Soon as we're done with the orchard.
Dumb bastard. Ah, I mean, yeah, we'll do it. Soon as we're done with the orchard. Thank you. With that, all of my current postings have been exhausted. Kismet be with you.
Thank you. With that, all of my current postings have been exhausted. Kismet be with you.

 Hi, Mister Count. We already know where the headwaters are.
Hi, Mister Count. We already know where the headwaters are. Ah, taking the initiative? Your guild never fails to impress me. Can you show me on your map where the headwaters are?
Ah, taking the initiative? Your guild never fails to impress me. Can you show me on your map where the headwaters are?
 This exclamation point.
This exclamation point. I shall have my scouts investigate there, then. Make yourselves comfortable while we await their results.
I shall have my scouts investigate there, then. Make yourselves comfortable while we await their results.
 ...
... ...
... ...
... ...
... We're not talking?
We're not talking? Ah, sorry, Harper, it's just been a long day. I'm kind of surprised you're not as exhausted as we are.
Ah, sorry, Harper, it's just been a long day. I'm kind of surprised you're not as exhausted as we are.
 It was nestled quite deep in the area you reported, but thanks to your information, we've found it at last. Thank you, Daffodil Guild. You have once again contributed to the development of our fair city. I have already contacted the Dancing Peacock about your reward.
It was nestled quite deep in the area you reported, but thanks to your information, we've found it at last. Thank you, Daffodil Guild. You have once again contributed to the development of our fair city. I have already contacted the Dancing Peacock about your reward. Yay. Thank you, Mister Count.
Yay. Thank you, Mister Count. No, thank you.
No, thank you.

 I had a feeling you would return quickly. The Count has informed me of your success—well done, Daffodil.
I had a feeling you would return quickly. The Count has informed me of your success—well done, Daffodil.


 Warding bells are consumables that are usable only in a dungeon. When used, they reduce the encounter rate for several steps. Useful if you have a quest you want to handle without getting into random encounters, I suppose.
Warding bells are consumables that are usable only in a dungeon. When used, they reduce the encounter rate for several steps. Useful if you have a quest you want to handle without getting into random encounters, I suppose.

 Hello, Lady Wynne. We're about to turn in for the day, but could you provide us with some information about your recent request before we do?
Hello, Lady Wynne. We're about to turn in for the day, but could you provide us with some information about your recent request before we do? Sure! See, I gots an idea to make some oils, but I need dragon's blood, which ya can take from da Small Orchard. Simple as dat.
Sure! See, I gots an idea to make some oils, but I need dragon's blood, which ya can take from da Small Orchard. Simple as dat.♪ No music ♪

 Man, I am bushed.
Man, I am bushed. Indeed, we have accomplished...quite a lot today.
Indeed, we have accomplished...quite a lot today. Oi, you lot're lookin' right knackered. What's the news?
Oi, you lot're lookin' right knackered. What's the news? A real bad fight with a baboon, and just generally walking through all of the first floor of the Lush Woodlands.
A real bad fight with a baboon, and just generally walking through all of the first floor of the Lush Woodlands. I feel quite accomplished! But also incredibly tired.
I feel quite accomplished! But also incredibly tired. Mm, mm, mm. Forests'll do that. Off where I come from, can't hardly take a quick jog without trippin' over a nasty flower or some rot.
Mm, mm, mm. Forests'll do that. Off where I come from, can't hardly take a quick jog without trippin' over a nasty flower or some rot. Where did you say you were from?
Where did you say you were from? Tell you later.
Tell you later. I'll make dinner. Buffalo steak with carrots. Maybe a carrot sauce.
I'll make dinner. Buffalo steak with carrots. Maybe a carrot sauce. ...Do you mind if I observe, Harper?
...Do you mind if I observe, Harper? No. Having someone else in the kitchen sounds nice.
No. Having someone else in the kitchen sounds nice. Thank you! I have found myself somewhat fascinated by cooking after having one of Miss Dalla's meals at the inn.
Thank you! I have found myself somewhat fascinated by cooking after having one of Miss Dalla's meals at the inn. She's a good cook.
She's a good cook. Later that night...
Later that night... ...Hm?
...Hm? Shhhhhhhit what were you thinking that bear could've not only mauled everyone but eaten them too that was so fucking dangerous it would've done even worse things than the baboon and that already knocked you flat on your ass that could've been it that could've been everyone's deaths—
Shhhhhhhit what were you thinking that bear could've not only mauled everyone but eaten them too that was so fucking dangerous it would've done even worse things than the baboon and that already knocked you flat on your ass that could've been it that could've been everyone's deaths— Uh, everything okay...?
Uh, everything okay...? Oh hey Merula what's up what're you doing up this late?
Oh hey Merula what's up what're you doing up this late? I was getting some water, but now I'm worried about you. You're...babbling.
I was getting some water, but now I'm worried about you. You're...babbling. Nah don't worry this just happens sometimes see the way I deal with stress is I just leave it for later y'know like I just put it in the back of my head and there I can get through the stressful stuff just fine I mean it does mean this happens to me later but I can deal with it.
Nah don't worry this just happens sometimes see the way I deal with stress is I just leave it for later y'know like I just put it in the back of my head and there I can get through the stressful stuff just fine I mean it does mean this happens to me later but I can deal with it. You say "don't worry," but... This isn't something I can not worry about. Please, take a deep breath.
You say "don't worry," but... This isn't something I can not worry about. Please, take a deep breath. I'm tellin' ya—
I'm tellin' ya— ...Please.
...Please. ...Haaah...
...Haaah... Haaaa...
Haaaa... Well? Are you feeling better?
Well? Are you feeling better? I mean. Not really. The stress is still in my head. But at least I can breathe.
I mean. Not really. The stress is still in my head. But at least I can breathe. Good. I'm glad. N-Not at the stress part, but at the breathing part.
Good. I'm glad. N-Not at the stress part, but at the breathing part. I, um... I didn't mean to intrude, so I'll be going now. If that's okay.
I, um... I didn't mean to intrude, so I'll be going now. If that's okay. Sure.
Sure. ...If things get bad, you can knock on my door. Don't worry, I'll answer. I hope you can get some sleep, Ace.
...If things get bad, you can knock on my door. Don't worry, I'll answer. I hope you can get some sleep, Ace. Gotcha. Thanks.
Gotcha. Thanks. Fffffffffuck, what were you thinking, dipshit...
Fffffffffuck, what were you thinking, dipshit...Next Update
Previous Update
Table of Contents